Problema45: Estimación y Pruebas de Hipótesis

Ej45. Una variable estudiada por los biólogos es la temperatura interna del cuerpo en los animales poiquilotermos (animales cuya temperatura corporal fluctúa con el ambiente circundante). El nivel letal (DL₅₀) para los lagartos del desierto es de 45ºC.

Se ha observado que la mayor parte de estos animales se oculta del calor en verano para evitar aproximarse a este nivel letal. Se realiza un experimento para estudiar X: “Tiempo (minutos) que se requiere para que la temperatura del cuerpo de un lagarto del desierto alcance los 45ºC partiendo de la temperatura normal de su cuerpo mientras está a la sombra”.

Se obtuvieron las siguientes observaciones:

10.1.

12.5.

12.2.

10.2.

12.8.

12.1.

11.2

11.4.

10.7.

14.9.

13.9.

13.3

Suponiendo X normal y a un nivel de significación de 0.05, determinar:

a) ¿Puede concluirse que el tiempo medio requerido para alcanzar la dosis letal es inferior a 13 minutos?.

b) ¿Puede concluirse que la desviación típica de X sea inferior a 1.5 minutos?.


En este problema, nos dan los datos de una muestra aleatoria, por lo que tenemos que obtener la media y la cuasi desviación estándar.

Para obtener la media:

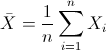
Por lo tanto:

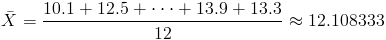
Para obtener la cuasi varianza:

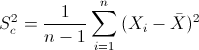
Por lo tanto:

S²_c ≈ 2.186288

Pasamos a resolver los distintos apartados que nos plantea el problema.


Apartado a)

Debemos obtener la prueba de hipótesis de la media con varianza desconocida:

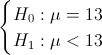
Es un contraste de media con desviación estándar desconocida, el estadístico es:

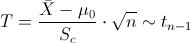
Obtenemos el valor del estadístico:

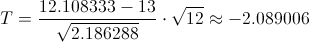
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

T ≤ - t_{α, n-1}

Para un nivel de significación de: α = 0.05, tenemos, en la tabla t-Student:

· t_{α, n-1} = t_{0.05, 12-1} = t_{0.05, 11} = 1.7959

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, -2.089006 es menor que el dato de la región crítica, -1.7959, por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

Esto quiere decir que, existen evidencias significativas de que el tiempo medio requerido para alcanzar la dosis letal es inferior a 13 minutos.

Para corroborar dicho análisis, vamos a obtener el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existe una región crítica, por lo tanto, tenemos una cola de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = P(T > |t|) = P(T > 2.089006)

Buscamos en las tablas de la t-Student con 11 grados de libertad, no encontramos el valor exacto, pero el valor más alto cercano al 2.089006 de las tablas corresponde al intervalo de área de cola:

0.025 < .p-valor < .0.05

Podemos dar un valor aproximado del p-valor realizando una interpolación lineal:

..0.05............X............0.025
1.7959...2.089006....2.2010

De donde:

0.05 - 0.025.-> 1.7959 - 2.2010
0.05 - X.-> 1.7959 - 2.089006

Calculamos:

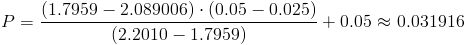
Por lo tanto, el p-valor es:

p-valor = P(T > 2.089006) = 0.031916

Al ser el nivel de significación del problema, α = 0.05, mayor que el p-valor, rechazamos la hipótesis nula y se acepta la hipótesis alternativa.


Apartado b)

La prueba de hipótesis que plantea el enunciado del problema es:

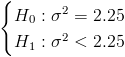
Es un contraste de varianza con media desconocida y sigue una distribución normal, el estadístico es:

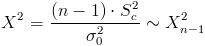
Aparte de obtener el p-valor, calcularemos también, la región crítica.

Antes que nada, obtenemos el valor del estadístico:

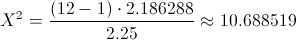
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

X² ≤ X²_{1-α, n-1}

Para un nivel de significación de: α = 0.05, tenemos, en la tabla ji-Cuadrada:

· X²_{1-α, n-1} = X²_{1-0.05, 12-1} = X²_{0.95, 11} = 4.57

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 10.688519 es mayor que el dato de la región crítica, 4.57, por lo tanto, aceptamos la hipótesis nula.

Ahora, vamos a obtener el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existe una región crítica, por lo tanto, tenemos una cola de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = P(X² > |x²|) = P(X² > 10.688519)

Buscamos en las tablas de la ji-Cuadrada con 11 grados de libertad, no encontramos el valor exacto, pero está dentro del los valores: 10.34 < . 10.688519 < . 12.9, cuya área de cola corresponde a: 0.3 < . α < . 0.5.

Por lo tanto, el p-valor estará comprendido entre los siguientes valores:

0.3 < . p-valor < . 0.5

Podemos dar un valor aproximado del p-valor realizando una interpolación lineal:

..0.5............X..............0.3
10.34...10.688519....12.9

De donde:

0.5 - 0.3.-> 10.34 - 12.9
0.5 - X.-> 10.34 - 10.688519

Calculamos:

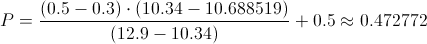
Por lo tanto, el p-valor es:

p-valor = P(X² > 10.688519) = 0.472772

Conclusión, el nivel de significación, α = 0.05, es más pequeño que el p-valor, por lo tanto, aceptamos la hipótesis nula.

Aceptar la hipótesis nula quiere decir que, existen evidencias significativas de concluir de que la desviación típica de X no es inferior a 1.5 minutos.