Problema81: Probabilidad

Ej81. Un investigador esta estudiando tres drogas D₁, D₂, D₃. Al inyectar las drogas a conejillos de indias, las probabilidades de que se forme una antitoxina son iguales a 1/4 para la nº 1, 1/8 para la nº 2 y 3/8 para la nº 3.

Hay 1 frasco de la nº 1, 3 de la nº 2 y 1 de la nº 3. El investigador toma un frasco al azar y con esta droga inyecta a un conejillo:

a) ¿Cuál es la probabilidad de que no se forme antitoxina?.

b) Si al conejillo no se le forma antitoxina, ¿cuál es la probabilidad de que la droga inyectada fuese la nº 2?.


Realizamos una recopilación de datos dados por el enunciado del problema:

· D₁ ≡ 'Droga nº1'. Hay 1 frasco para este tipo de droga.
· D₂ ≡ 'Droga nº2'. Hay 3 frascos para este tipo de droga.
· D₃ ≡ 'Droga nº3'. Hay 1 frasco para este tipo de droga.

En total, existen: 1+3+1 = 5 frascos.

· P(D₁) = 1/5
· P(D₂) = 3/5
· P(D₃) = 1/5

· E ≡ 'Se forma antitoxina'.

· P(E|D₁) = 1/4.
· P(E|D₂) = 1/8.
· P(E|D₃) = 3/8.

Pasamos a resolver los distintos apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden la probabilidad de que no se forme antitoxinas, calcularemos su complementario, que se formen antitoxinas, ya que disponemos los datos acorde a esta probabilidad y una vez obtenida, obtendremos el que nos he requerido por el enunciado.

Emplearemos la expresión de la probabilidad total, para obtener la probabilidad de que se forme antitoxinas.

P(E) = P(E|D₁)·P(D₁) + P(E|D₂)·P(D₂) + P(E|D₃)·P(D₃) = (1/4)·(1/3) + (1/8)·(3/5) + (3/8)·(1/5)

Operamos:

P(E) = 7/30

Por lo tanto, la probabilidad de no formarse antitoxina es el complementario:

P(Ē) = 1 - P(E) = 1 - 7/30 = 23/30

Por lo tanto, la probabilidad de que no se forme antitoxina es de, aproximadamente 0.766667.


Apartado b)

En este apartado nos piden obtener la probabilidad de que dado que no se forme antitoxinas, sea de la droga nº2, emplearemos para tal fin la Ley de Bayes:

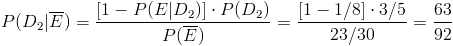
Por lo tanto, la probabilidad de que dado que no se forme antitoxinas, sea de la droga nº2 es de, aproximadamente 0.684783.