Ej57. Supóngase que en cierto organismo vivo sometido a un tipo de radiación se están produciendo células tumorales con una tasa promedio de 5 cada minuto.
Es de interés conocer ciertas probabilidades en relación a la producción de dichas células. Determinar:
a) Si la producción de células tumorales por minuto supera el valor de 3 se considera situación de alerta moderada. ¿Qué probabilidad hay de que esto suceda?.
b) Calcular la probabilidad de que el número de células tumorales producidas no sea superior a 2.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Nº de células tumorales producidas'.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(5).
Apartado a)
Debemos obtener la siguiente probabilidad:
Al tener que calcularse el valor de varios elementos para obtener la solución a este apartado, vamos a emplear el software R para realizar dicha operación:
> 1-ppois(3,5)
[1] 0.7349741
Por lo tanto, la probabilidad de alerta moderada es de, aproximadamente, 0.734974.
Apartado b)
La probabilidad que debemos obtener es la siguiente:
Sustituimos valores:
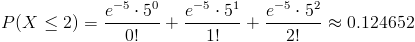





0 comentarios:
Publicar un comentario