Problema65: VAC

Ej65. Se estima que una enfermedad vírica se consigue curar sin secuelas en un 1% de los casos. A un bioestadístico se le plantea el problema de valorar la probabilidad de que en una muestra de tamaño 1000 se produzcan más de 12 curaciones.


Realizamos una recopilación de datos que nos ofrece el enunciado:

· Sea la variable aleatoria X, número de curaciones sin secuelas de una enfermedad vírica.
· Tamaño de la muestra: N = 1000 individuos.
· La variable aleatoria discreta X sigue una distribución binomial: X ~ B(1000, 0.01)

Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:

1. n·p ≥ 5 → 1000·0.01 = 10 ≥ 5 OK.

2. n·q ≥ 5 → 1000·(1-0.01) = 990 ≥ 5 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

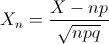
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(10, √9.9).

Debemos obtener la siguiente probabilidad:

P(X > 12)

Aplicamos el factor de corrección:

P(X > 12.5)

Y en estos momentos estamos en condiciones de tipificar por la Normal:

Aproximadamente es:

P(X > 12.5) ≈ P(Z > 0.79) = 1 - P(Z ≤ 0.79) = 1 - [0.5 + Φ(0.79)] = 0.5 - Φ(0.79)

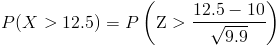
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:

P(X > 12.5) ≈ P(Z > 0.79) = 0.5 - Φ(0.79) = 0.5 - 0.2852 = 0.2148

Por lo tanto, la probabilidad de que en una muestra de tamaño 1000, se produzcan más de doce curaciones sin secuelas, es de 0.2148.