Ej64. Sea X la cantidad de radiación que puede ser absorbida por un individuo antes de que le sobrevenga la muerte. Supongamos que X es Normal con una media de 500 roentgen y una desviación típica de 150 roentgen.
Determinar:
a) ¿Por encima de qué nivel de dosificación sobreviviría solamente el 5% de los expuestos?.
b) ¿Cuál es el porcentaje de supervivientes para un nivel de radiación de 800 roentgen?.
Sea la variable aleatoria X, cantidad de radiación que puede ser absorbida por un individuo antes de que le sobrevenga la muerte. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Por lo tanto: X ~ N(500, 150) roentgen.
Pasamos a resolver los distintos apartados del problema.
Apartado a)
En este problema, nos dan los datos de la probabilidad y debemos hallar el valor de la media de la variable aleatoria X que lo satisfaga.
Tenemos: P(X > x) = 1 - P(X ≤ x) = 0.05
Por lo tanto, debemos obtener la probabilidad siguiente:
Tipificamos:
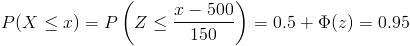
Despejamos:
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..1.64.............Z..........1.65
0.4495........0.45.....0.4505
De donde:
1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45
Calculamos:
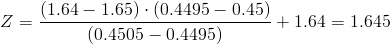
Por lo tanto, tenemos:
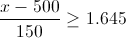
Despejamos la variable a determinar, para obtener la solución a este apartado:
Por lo tanto, el nivel de dosificación requerido para cumplir los requisitos expuestos por el enunciado del apartado es de 746.75 roentgen.
Apartado b)
En este apartado, debemos obtener la probabilidad de supervivencia, pero vamos a obtener el complementario ya que tenemos los datos y las variables definidas para tal fin:
Tipificamos:
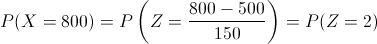
Operamos:
Una vez obtenida la probabilidad de mortalidad para los requisitos expuestos en este apartado, vamos a obtener lo que realmente nos exigen, la supervivencia:
· (1-0.9772)·100 = 2.28%
Por lo tanto, el porcentaje de supervivientes para un nivel de radiación de 800 roentgen es de 2.28%.





4 comentarios:
Hola manuel, felicidades por el blog. Quería preguntarte por el apartado a). A la hora de tipificar no entiendo que significa o de dónde sale 0,5+ (z).¿ Podrías aclarármelo por favor?
Gracias
Buenas Julián:
El 0.5 dichoso es por las tablas de la Normal que en este blog empleamos para resolver este tipo de problemas.
Si te fijas en la tabla de la Normal, verás que la curva (la campana de Gauss) está centrada, es decir, el eje de coordenadas Y está justamente en el medio de la curva.
¿Qué efectos tiene poner dicho eje en esa posición? Pues fácil, sólo empleamos la mitad de la curva. Esto se puede hacer así ya que la campana de Gauss es una curva simétrica.
Por lo tanto, cuando obtenemos una probabilidad debemos añadir la otra mitad de la curva que no tenemos en consideración, y éste es el valor de 0.5.
Te recomiendo, para que lo veas más claro, que te pases por el apartado de la Normal (en el apartado de tablas), dónde encontrarás ejercicios jugando con este tipo de curva matemática.
Un saludo y gracias por tu comentario.
Buenas tardes, muy buen blog.
Verás no se de donde sale el 1,64, del apartado a)
Buenas:
A la hora de tipificar los datos y buscarlo en la Tabla de la Normal, no tenemos el resultado exacto, por lo que necesitamos realizar interpolación.
Para ello, cogemos el valor inmediatamente inferior y superior al valor que queremos hallar, y es ahí, donde sale el 1.64, es el valor inferior.
Te recomiendo que te mires los ejercicios de trabajar con la Tabla de la Normal que tenemos en el blog.
Un saludo.
Publicar un comentario