Problema 41: Estimación y Prueba de Hipótesis

Ej41. Durante un año se registran los siguientes pedidos:

	Zona Norte.	Zona Centro.	Zona Sur.
Aluminio	301	635	345
Acero	49	115	55

Determinar, teniendo en cuenta un nivel del 95%:

a) Hallar un intervalo de confianza para la proporción de pedidos del material de Aluminio que recibe la fábrica.

b) Se afirma que la proporción de pedidos del material de Aluminio de la zona Norte es la misma que la proporción de pedidos del material de Aluminio de la zona Sur. ¿Podemos aceptar dicha afirmación?.


Apartado a)

Realizamos un recopilatorio de los datos ofrecidos en el enunciado del apartado:

· X ≡ 'Proporción del material de aluminio que recibe la fábrica'.
· P(X) = (301+635+345)/[(301+635+345)+(49+115+55)] = 0.854.

Nos pide realizar un intervalo de confianza de proporción, debemos verificar las siguientes condiciones:

· n = (301+635+345)+(49+115+55) = 1500 ≥ 30 OK.
· n·p = 1500·(0.854) = 1281 ≥ 5 OK.
· n·q = 1500·(1-0.854) = 219 ≥ 5 OK.

Por lo tanto, el intervalo de confianza a obtener es el siguiente:

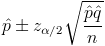
Para un 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: z = 1.96.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la proporción de familias con coche al 95%, simplemente, sustituimos valores:

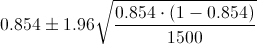
El intervalo de confianza es:

[0.836130, 0.871870]

Apartado b)

En este apartado, debemos dar como respuesta si las proporciones de pedidos del material de aluminio son las mismas para la zona norte y la zona sur. Para tal fin, realizaremos una prueba de hipótesis.

Pero antes, recopilamos información de ambas zonas:

· A ≡ 'Proporción del material de aluminio que recibe la fábrica de la zona norte'.
· P(A) = 301/(301+49) = 301/350 = 0.86.

· B ≡ 'Proporción del material de aluminio que recibe la fábrica de la zona sur'.
· P(B) = 345/(345+55) = 345/400 = 0.8625.

Debemos verificar las siguientes condiciones:

· n₁ = 350 ≥ 30 OK.
· n₂ = 400 ≥ 30 OK.
· n₁·p₁ = 350·(0.86) = 301 ≥ 5 OK.
· n₂·p₂ = 400·(0.8625) = 345 ≥ 5 OK.
· n₁·q₁ = 350·(1-0.86) = 49 ≥ 5 OK.
· n₂·q₂ = 400·(1-0.8625) = 55 ≥ 5 OK.

Tomo como hipótesis nula que ambas proporciones son iguales, siendo la hipótesis alternativa, que no lo son:

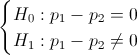
Cuyo estadístico es:

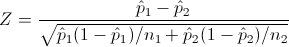
Ya disponemos de los datos necesarios para obtener el valor del estadístico:

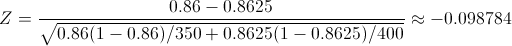
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ - z_α/2, Z ≥ z_α/2

Para un nivel de significación de: α = 0.05, tenemos, en la tabla Normal:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: Z = 1.96.

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, -0.098784 está dentro del intervalo que compone la región crítica, (-1.96, 1.96), por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que ambas proporciones son iguales, por lo tanto, podemos aceptar dicha afirmación.

Para corroborar nuestra afirmación, obtendremos el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2 · P(Z > |z|) = 2 · P(Z > 0.098784) = 2·[1 - P(Z ≤ 0.098784)] = 2·[1 - (0.5 + Φ(0.098784))] = 2·[0.5 - Φ(0.098784)]

Buscamos en las tablas de la Normal, pero no encontramos el valor exacto para 0.098784, por lo que interpolamos linealmente:

..0.09...........0.098784.......0.10
0.0359...............P............0.0398

De donde:

0.09 - 0.10.-> 0.0359 - 0.0398
0.09 - 0.098784.-> 0.0359 - P

Calculamos:

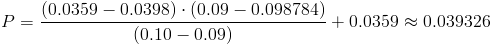
Sustituimos y obtenemos el p-valor:

p-valor = 2·[0.5 - Φ(0.098784)] = 2·[0.5 - 0.039326] = 0.921348

Como el p-valor es mayor que el nivel de significación, aceptamos la hipótesis nula, esto corrobora el resultado obtenido mediante la región crítica.