Problema59: VAC

Ej59. Un transportista cuando llega a la fábrica tiene que descargar el material transportado. El tiempo de espera hasta que es atendido X₁ es una variable aleatoria distribuida uniformemente en (0, 1).

El tiempo que tarda en descargar X₂ se distribuye en forma exponencial con parámetro medio 0.5.

Los tiempos X₁ y X₂ son independientes y se miden en horas. Sean los sucesos A ≡ 'Tiempo de espera es inferior a 0.75 horas' y B ≡ 'Tiempo de descarga es superior a 0.5 horas'.

Hallar la probabilidad P(A ∪ B).


Realizamos una recopilación de datos que nos ofrece el problema:

· X₁ ≡ 'Tiempo de espera hasta que es atendido'.
· La variable X₁ se distribuye de forma uniforme: X₁ ~ U(0, 1)

· X₂ ≡ 'Tiempo que tarda en descargar'.
· La variable X₂ se distribuye de forma exponencial: X₂ ~ Exp(0.5)

· Ambas variables aleatorias son independientes entre sí.

Nos ofrecen dos eventos:

· A ≡ 'Tiempo de espera es inferior a 0.75 horas'.
· Dicho suceso sigue una distribución uniforme cómo en la variable aleatoria X_1.

Para resolver dicho evento, empleamos la función de distribución acumulada de la distribución uniforme:

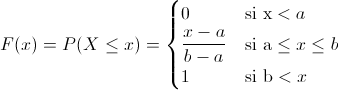
Por lo tanto:

F(A) = P(X₁ < .0.75) = (0.75-0)/(1-0) = 0.75.

Y para el otro evento que nos dicta el enunciado del problema:

· B ≡ 'Tiempo de descarga es superior a 0.5 horas'.
· Dicho suceso sigue una distribución exponencial cómo en la variable aleatoria X2.

Debemos emplear la función de distribución acumulada de la distribución exponencial:

Por lo tanto:

P(X₂ >.0.5) = 1 - P(X₂ ≤ 0.5) = 1 - [1 - e^-0.5/0.5] = e^-1 ≈ 0.367879

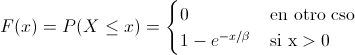
En estos momentos, podemos obtener la probabilidad que nos piden en este problema:

P(A ∪ B) = P(A) + P(B) - P(A∩B)= 0.75 + 0.367879 - 0.75·0.367879 ≈ 0.841970

Por lo tanto, la solución es, 0.841970.