Problema74: Probabilidad

Ej74. En una ciudad el 40% de las personas tienen el pelo rubio, el 25% los ojos azules y el 15% el pelo rubio y los ojos azules. Se selecciona una persona al azar.

Calcular las siguientes probabilidades:

a) Tener el pelo rubio si tiene los ojos azules.

b) Tener los ojos azules si tiene el pelo rubio.

c) No tener el pelo rubio ni los ojos azules.

d) Tener exactamente una de estas dos características.


Realizamos una recopilación de datos dados por el enunciado del problema:

· E ≡ 'Tiene pelo Rubio'.
· O ≡ 'Tiene ojos Azules'.

· P(E) = 0.4.
· P(O) = 0.25.
· P(E∩O) = 0.15.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de que al escoger un individuo al azar, éste tenga el pelo rubio dado que posee los ojos azules:

Por lo tanto, la probabilidad de que el individuo tenga el pelo rubio dado que posea los ojos azules es de 0.6.


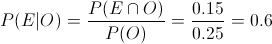
Apartado b)

En este apartado nos piden obtener la probabilidad de que al escoger un individuo al azar, éste tenga los ojos azules dado que posee el pelo rubio:

Por lo tanto, la probabilidad de que el individuo tenga los ojos azules dado que posea el pelo rubio es de 0.375.


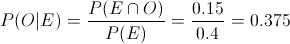
Apartado c)

En este apartado nos piden obtener la probabilidad de que ni tenga el pelo rubio ni los ojos azules:

P(Ē ∩ Ō) = P[(1-E) ∩ (1-O)] = 1 - P(E) - P(O) + P(E∩O) = 1 - 0.4 - 0.25 + 0.15 = 0.5

Por lo tanto, la probabilidad de que no tenga el pelo rubio ni los ojos azules es de 0.5.


Apartado c)

En este apartado nos piden obtener la probabilidad de que o tenga el pelo rubio o los ojos azules exactamente:

P[Ē ∩ O) ∪ (E ∩ Ō)] = P(E) + P(O) - 2·P(E∩O) = 0.4 + 0.25 - 2·0.15 = 0.35

Por lo tanto, la probabilidad de que o tenga el pelo rubio o los ojos azules exactamente es de 0.35.