Ej58. Los distribuidores de una fábrica clasifican sus pedidos atendiendo al material Aluminio y Acero y a la zona de procedencia Zona Norte, Zona Centro y Zona Sur.
El número de pedidos X es una variable de Poisson de parámetro 267 pedidos/mes, determinar:
a) Hallar la probabilidad de que en un mes se reciban a lo más, 250 pedidos.
b) Hallar la probabilidad de que en dos meses se reciban a lo más, 500 pedidos.
Realizamos una recopilación de datos que nos ofrece el enunciado:
· Sea la variable aleatoria X, número de pedidos por mes.
· La variable aleatoria discreta X sigue una distribución Poisson: X ~ P(267)
Pasamos a resolver los apartados que nos ofrece el enunciado del problema.
Apartado a)
Debemos obtener la siguiente probabilidad:
Determinaremos, si se puede aproximar a la Normal, para ello, se deben cumplir la siguiente condición:
1. λ > 25 → 267 > 25 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
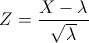
Por lo tanto: X ~ N(λ, √λ) = N(267, √267).
Aplicamos el factor de corrección:
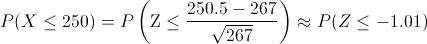
Obtenemos:
Por lo tanto, la probabilidad de que en un mes se reciban como máximo 250 pedidos, es de 0.1562.
Apartado b)
Debemos obtener la siguiente probabilidad:
Tenemos que adaptar nuestro parámetro promedio ya que el estudio está basado en dos meses:
..1....--- 267
..2....--- λ
Por lo tanto, el número medio de pedidos/mes es:
· λ = (2·267)/1 = 534
Determinaremos, si se puede aproximar a la Normal, para ello, se deben cumplir la siguiente condición:
1. λ > 25 → 534 > 25 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
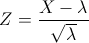
Por lo tanto: X ~ N(λ, √λ) = N(534, √534).
Aplicamos el factor de corrección:
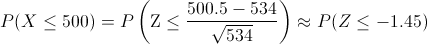
Obtenemos:
Por lo tanto, la probabilidad de que en dos meses se reciban como máximo 500 pedidos, es de 0.0735.





0 comentarios:
Publicar un comentario