Ej49. En un anuncio publicitario se indica que un determinado tipo de agua reduce peso. Doce individuos que decidieron tomar dicha agua en sustitución de la que tomaban habitualmente, manteniendo intacta el resto de la dieta alimenticia sufrieron las siguientes variaciones de peso al cabo de cierto tiempo:
Individuo
| 1
| ..2.
| ..3.
| 4
| 5
| 6
| 7
| 8
| ..9.
| 10
| 11
| 12
|
Variación del Peso
| 0.2
| 0
| 1
| 0.6
| -0.5
| -0.06
| -1
| 0.6
| 1
| 0.5
| -0.4
| -0.5
|
Teniendo en cuenta estos datos y a un nivel de significación del 0.05, ¿se puede afirmar la veracidad del anuncio?.
En este problema, nos dan los datos de una muestra aleatoria, por lo que tenemos que obtener la media y la cuasi desviación estándar.
Para obtener la media:
Por lo tanto:
·
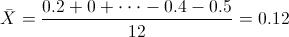
Para obtener la cuasi varianza:
Por lo tanto:
· Sc = 0.639659
La prueba de hipótesis que plantea el enunciado del problema es:
Es un contraste de media con desviación estándar desconocida, el estadístico es:
Obtenemos el valor del estadístico:Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
T ≤ - tα/2, n -1, T ≥ tα/2, n -1
Para un nivel de significación de: α = 0.05, tenemos, en la tabla t-Student:
· tα/2, n -1 = t0.05/2, 12 -1 = t0.025, 11 = 2.2010
Comprobamos el valor del estadístico con la región crítica:
El valor del estadístico, 0.649865 está dentro del intervalo que compone la región crítica, (-2.2010, 2.2010), por lo tanto, aceptamos la hipótesis nula.
Esto quiere decir que existe evidencias significativas de que la media es cero, por lo tanto, no podemos decir que el anuncio sea correcto.
Para refutar el anterior análisis, vamos a obtener el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:
p-valor = 2 · P(T > |t|) = 2 · P(T > 0.649865) ≈ 2 · P(T > 0.6499)
Buscamos en las tablas de la t-Student con 11 grados de libertad, no está el valor exacto, pero está dentro del los valores: 0.5399 < . 0.6499 < . 0.6974, cuya área de cola corresponde a: 0.25 < . α < . 0.3.
Teniendo en cuenta que existen dos áreas de cola, el
p-valor estará comprendido entre los valores:
0.5 < . p-valor < . 0.6
Podemos dar un valor aproximado del
p-valor realizando una interpolación lineal:
..0.300
.......P
.........0.250
0.5399
...0.6499
..0.6974
De donde:
0.300 - 0.250
.-> 0.5399 - 0.6974
0.300 - P
.-> 0.5399 - 0.6499
Calculamos:
Por lo tanto, el p-valor es:
p-valor = 2 · P(T > 0.6499) = 2 · 0.265079 = 0.530158
Al ser el nivel de significación del problema, α = 0.05, menor que el p-valor, aceptamos la hipótesis nula. Por lo tanto, queda demostrado el estudio realizado anteriormente mediante la región crítica y por ende, la veracidad del anuncio es más que dudosa.
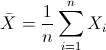
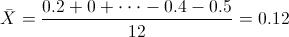
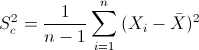
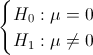
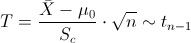
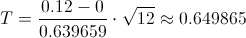
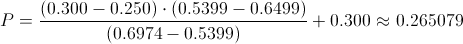






2 comentarios:
¿por qué si el anuncio dice que reduce el peso, las hipótesis son igual o distinto? no entiendo muy bien lo de los signos de desigualdad de las hipótesis, se lo agradecería infinito si pudiera explicarlo. gracias de antemano
Buenas José María Becerra:
El anuncio dice que un determinado tipo de agua reduce peso, entonces ¿por qué hemos elegido el contraste de hipótesis nula donde la media es igual a cero y la hipótesis alternativa distinta de cero?
Es simple, si el resultado obtenido del estudio nos indica que la media es cero ( tal como hemos podido comprobar en el desarrollo del problema ), nos quiere decir que no hay cambio de peso entre los individuos estudiados a ese nivel de significación y si su masa no ha cambiado, el anuncio es dudoso al afirmar que reduce peso.
Imaginemos que cuando estamos desarrollando el problema, el resultado hubiese sido distinto, es decir, rechazamos la hipótesis nula ( la masa es cero ), y aceptamos la alternativa ( la masa es distinta de cero ), ¿qué hubiese querido decir? Pues con este resultado, tampoco estaríamos en disposición de afirmar que se reduce peso con ese tipo de agua, solo que el peso cambia a ese nivel de significación, por lo tanto, podría reducir peso o aumentar peso.
Para determinar si se engorda o se adelgaza, necesitaríamos un dato añadido para comparar y realizar otro estudio de hipótesis, pero el enunciado es el que es, y con lo que tenemos, solo podemos realizar este tipo de test: si se cambia de peso o no.
Si tienes dudas, me lo dices e intento ser más claro.
Un saludo.
Publicar un comentario