Problema55: Estimación y Pruebas de Hipótesis

Ej55. Se quieren comparar dos métodos, A y B, para determinar el calor latente de fusión del hielo. La siguiente tabla da los resultados obtenidos (en calorías por gramo de masa para pasar de –0.72ºC a 0ºC) usando reiteradamente ambos métodos:

A	79.98	80.04	80.02	80.04	80.03	80.03	80.04	79.97	80.05	80.03
B	80.02	79.94	79.98	79.97	79.97	80.03	79.95	79.97

Considerando normalidad e independencia, obtener un intervalo de confianza al nivel 95% para comparar las mediciones medias obtenidas por ambos métodos.


Recopilamos y obtenemos datos que nos serán de utilidad para posteriormente, resolver los distintos apartados.

Para obtener la media:

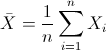
Por lo tanto:

·

·

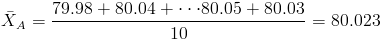
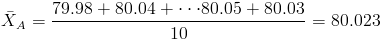
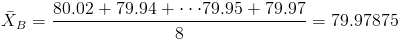
Para la cuasi desviación típica de cada muestra:

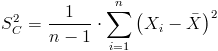
Para cada método, las desviaciones estándar son:

· S²_cA ≈ 0.000712

· S²_cB ≈ 0.000984

Para un 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05.

Nos piden obtener un intervalo de confianza para la diferencia de medias de ambos métodos, pero nos encontramos con un problema, las varianzas son desconocidas de ambas muestras pero no sabemos si son iguales o no. Esto es importante ya que dependiendo de dicho matiz, cambia la forma de resolver el problema.

Por lo tanto, lo primero que debemos hacer, es una prueba de hipótesis para dictaminar si ambas varianzas desconocidas son iguales o no.

Tomo como hipótesis nula que ambas varianzas son iguales, siendo la hipótesis alternativa, que no lo son:

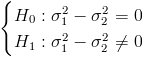
Cuyo estadístico es:

Ya disponemos de los datos necesarios para obtener el valor del estadístico:

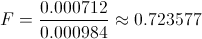
Para ver si aceptamos la hipótesis nula, debemos calcular la región crítica y evaluar los resultados obtenidos. La región crítica para este estudio es:

F ≥ F_{α/2,n1-1,n2-1} , F ≤ F_{1-α/2, n1-1,n2}-1

Para un nivel de significación de: α = 0.05, buscamos en tabla distribución F:

· f_{1-α/2,n1-1,n2-1} = f_{1-0.05/2,10-1, 8-1} = f_0.975,9,7 = 1/f_1-0.975,7,9 = 1/f_0.025,7,9 = 1/4.20 ≈ 0.238095

· f_{α/2,n1-1,n2-1} = f_{0.05/2,10-1,8-1} = f_0.025,9,7 = 4.82

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 0.723577 está dentro de la marcada por la región crítica, [0.238095, 4.82], por lo tanto, aceptamos la hipótesis nula.

Una vez que sabemos que la varianza de ambas muestras son iguales, pasamos a confeccionar el intervalo de confianza para la diferencia de medias.

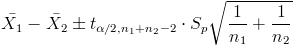
El siguiente paso es obtener los valores de:

· t_α/2,n1+n2-2 = t_{0.05/2,10+8-2}=t_{0.025, 16}

Buscamos el valor en la tabla t-Student, y obtenemos: 2.1199.

Necesitamos obtener el valor de Sp:

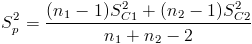
Sustituimos valores:

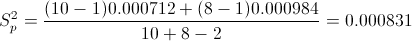
Ya disponemos todos los datos necesarios para obtener el intervalo bilateral de confianza al 95% de la diferencia de medias con varianzas desconocidas e iguales:

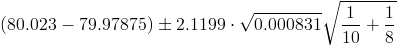
El intervalo de confianza bilateral al 95% es:

[0.015263, 0.073237]