Problema65: VAD

Ej65. De 60 aspirantes a una universidad 40 son del oriente, si se seleccionan 20 aspirantes aleatoriamente, hallar la probabilidad de que:

a) 10 sean del oriente.

b) No más de 2 sean de oriente.

Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº aspirantes a la universidad que son de oriente'.
· La variable aleatoria X sigue una distribución Hipergeométrica: X ~ HG de parámetros:
· Número total de aspirantes: N = 60.
· Tamaño de la muestra: n = 40. (Número total de aspirantes orientales)
· Número total de aspirantes seleccionadas aleatoriamente: r = 20.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.

Apartado a)

Debemos hallar la siguiente probabilidad:

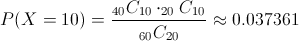
Por lo tanto, la probabilidad de que diez aspirantes sean orientales es de, aproximadamente, 0.037361.

Apartado b)

Debemos hallar la siguiente probabilidad:

P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

Para tal fin, emplearemos el software R:

> sum(dhyper(c(0, 1, 2), 40, 60-40, 20))
[1] 3.554545e-11

Por lo tanto, la probabilidad de que a lo sumo dos aspirantes sean orientales es de, aproximadamente, 3.55·10^-11, prácticamente improbable.