Problema66: VAD

Ej66. Suponga que el número de llamadas que llegan a un conmutador es de 0.5 por minuto en promedio, halle la probabilidad de que:

a) En un minuto lleguen más de 3 llamadas.

b) En un minuto no lleguen llamadas.

c) En 3 minutos lleguen menos de 5 llamadas.

d) En 5 minutos más de 2 llamadas.

e) ¿Cuántas llamadas se espera que lleguen al conmutador en cinco minutos?.


Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de llamadas que llegan a un conmutador'.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(0.5) por minuto.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.

Apartado a)

Debemos obtener la siguiente probabilidad:

P(X > 3) = 1 - P(X ≤ 3) = 1 - [P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)]

Al tener que calcularse el valor de varios elementos para obtener la solución a este apartado, vamos a emplear el software R para realizar dicha operación:

> 1-ppois(3, 0.5)
[1] 0.001751623

Por lo tanto, la probabilidad de que lleguen más de tres llamadas es de, aproximadamente, 0.001752.

Apartado b)

La probabilidad que debemos obtener es la siguiente:

Por lo tanto, la probabilidad de que no se reciban llamadas es de, aproximadamente, 0.606531.

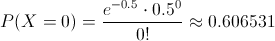
Apartado c)

Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en 0.5 llamadas por minuto:

..0.5..--- 1
.....λ...--- 3

Por lo tanto, el número medio de llamadas recibidas en tres minutos es:

· λ = (0.5·3)/1 = 1.5

La probabilidad que debemos obtener es la siguiente:

P(X < .5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)

Al tener que calcularse el valor de varios elementos para obtener la solución a este apartado, vamos a emplear el software R para realizar dicha operación:

> sum(dpois(c(0, 1, 2, 3, 4), 1.5))
[1] 0.981424

Por lo tanto, la probabilidad de que lleguen menos de cinco llamadas cada tres minutos es de 0.981424.

Apartado d)

Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en 0.5 llamadas por minuto:

..0.5..--- 1
.....λ...--- 5

Por lo tanto, el número medio de llamadas recibidas en cinco minutos es:

· λ = (0.5·5)/1 = 2.5

La probabilidad que debemos obtener es la siguiente:

P(X > 2) = 1 - P(X ≤ 2) = 1 - [P(X = 0) + P(X = 1) + P(X = 2)]

Al tener que calcularse el valor de varios elementos para obtener la solución a este apartado, vamos a emplear el software R para realizar dicha operación:

> 1-ppois(2, 2.5)
[1] 0.4561869

Por lo tanto, la probabilidad de que lleguen más de dos llamadas cada cinco minutos es de, aproximadamente 0.456187.

Apartado e)

Para obtener el promedio de llamadas que recibirá el conmutador simplemente, debemos adaptar nuestro parámetro:

..0.5..--- 1
.....λ...--- 5

Por lo tanto, el número medio de llamadas recibidas en cinco minutos es:

· λ = (0.5·5)/1 = 2.5

Por lo tanto, el número promedio de llamadas que recibirá el conmutador en cinco minutos es de 2.5.