Problema26: Análisis de Regresión

Ej26. Un estudio hecho por el departamento de transporte de Atlanta, Georgia, acerca del efecto de los precios de los boletos de los autobuses sobre el número de pasajeros produjo los siguientes resultados:

X	25	30	35	40	45	50	55	60
Y	800	780	780	660	640	600	620	620

Dónde:

· X ≡ Precio del boleto en centavos.
· Y ≡ Pasajeros por 100 millas.

Obtener:

a) Encuentra la recta de regresión que relaciona ambas variables.

b) Obtener el estimador de la variación estándar.

c) Pronostique el número de pasajeros por 100 millas si el precio del boleto fuera de 50 centavos.


Antes de empezar a resolver los apartados propuestos, hacemos una recopilación de datos que podemos extraer de la tabla dada, ya que posteriormente serán de gran utilidad.

· n = 8

·

·

·

·

·

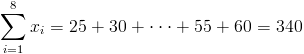
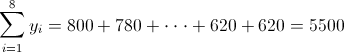
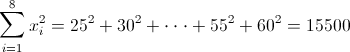
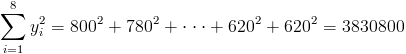
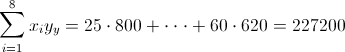
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

Para calcular la pendiente, la expresión matemática es:

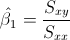
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:

·

·

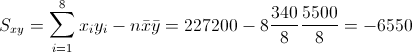
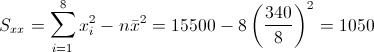
Por lo tanto, la pendiente es:

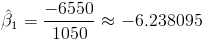
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:

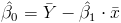
Sustituimos valores:

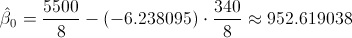
Por lo tanto, la ecuación de regresión ajustada es:

y(x) = 952.619038 - 6.238095·x

Apartado b)

Debemos obtener el valor del estimador de la desviación estándar:

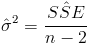
Siendo:

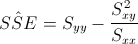
Debemos obtener Syy:

·

Ya tenemos todos los datos necesarios para estimar la varianza:

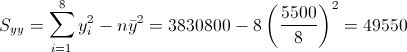
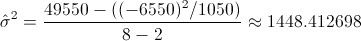
Por lo tanto, el estimador de la variación estándar es, aproximadamente 38.058018.


Apartado c)

En este apartado, debemos obtener el valor mediante la recta ajustada.

y(x) = 952.619038 - 6.238095·x

· Para Precio del boleto = 50 centavos:

y(50) = 952.619038 - 6.238095·50 = 640.714288