Problema74: Estimación y Pruebas de Hipótesis

Ej74. Se quiere comparar rodamientos de agujas de 45 mm de diámetro de dos fabricantes distintos: SKF e INA. Una característica de la calidad de los rodamientos es su capacidad estática de carga, que es la carga máxima que puede soportar sin que se produzca deformación.

Se toma una muestra de 80 rodamientos del SKF y 67 de INA. Sea X₁ la capacidad estática de carga de los rodamientos de SKF y X₂ la capacidad estática de carga de los rodamientos de INA.

La media muestral de la capacidad estática de carga de SKF es de 1400 kN, y la de INA es 1380 kN. Las varianzas de X₁ y de X₂ son iguales y tiene un valor conocido de 90² kN.

Construye un intervalo de confianza del 95% de la diferencia de medias poblacionales.


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· X₁ ≡ 'Capacidad estática de carga de los rodamientos de la fábrica SKF'. Sigue una distribución Normal: X₁ ~ N(1400, √90), n₁ = 80.
· X₂ ≡ 'Capacidad estática de carga de los rodamientos de la fábrica INA'. Sigue una distribución Normal: X₁ ~ N(1380, √90), n₂ = 67.

Nos pide realizar un intervalo de confianza para la diferencia de medias con varianzas conocidas:

Para un 95%, obtenemos α:

100(1 - α) = 95

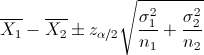
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es 1.96.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la diferencia de medias con un 95%, simplemente, sustituimos valores:

Por lo tanto, el intervalo de confianza requerido por el enunciado del problema es, aproximadamente:

[-9.212912, 49.212912]

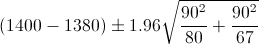
Como podemos comprobar, el intervalo contiene el número cero, por lo tanto, podemos determinar que dicho estudio no es significativo ya que no podemos precisar que cantidad de carga estática de los rodamientos de cada fábrica es mayor o menor.