Problema42: Estimación y Pruebas de Hipótesis

Ej42. Ante la sospecha de una diferencia sistemática entre dos laboratorios A y B a la hora de determinar la cantidad de albúmina sérica, expresada en gr./100 ml., se ha realizado una experiencia consistente en la extracción de sangre a 10 pacientes.

Para cada muestra de sangre se midió tal proteína en ambos laboratorios y las diferencias entre laboratorios (A–B) fueron las siguientes:

0.6.

0.7.

0.8.

0.9.

0.3.

0.5.

-0.5.

1.3..

0.4..

1.8

Considerando normalidad, calcular un intervalo de confianza para la diferencia media de medición al 90% considerando que la desviación típica de las diferencias poblacionales es 0.22.


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· Desviación estándar: σ = 0.22.
· Tamaño de la muestra: n = 10.
· D ≡ 'Diferencia entre los laboratorios A-B'.

Para obtener la media:

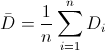
Por lo tanto:

·

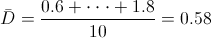
La variable aleatoria D, sigue una distribución Normal: D ~ N(0.58, 0.22)

Nos piden realizar un intervalo de confianza para la diferencia de medias con varianza conocida:

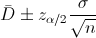
Para una confianza del 90%, obtenemos α:

100(1 - α) = 90

Despejamos el parámetro que nos interesa: α = 0.1. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.1/2 = z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:

..1.64.............Z..........1.65
0.4495........0.45.....0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45

Calculamos:

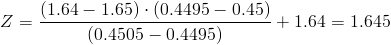
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la diferencia de medias con un 90%, simplemente, sustituimos valores:

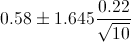
El intervalo de confianza bilateral al 90% es, aproximadamente:

[0.465557, 0.694443]