Problema77: Probabilidad

Ej77. En un laboratorio hay 3 cajas. La caja 1ª contiene 2 cobayas marrones y 3 blancas, la 2ª caja 4 marrones y 2 blancas y la 3ª caja 5 marrones y 5 blancas.

Se elige una caja al azar y se extrae una cobaya:

a) Calcular la probabilidad de que la cobaya elegida sea blanca.

b) Si la cobaya elegida resulta ser blanca, ¿cuál es la probabilidad de que proceda de la primera caja?.


Realizamos una recopilación de datos dados por el enunciado del problema:

· M ≡ 'Cobaya de color marrón'.
· B ≡ 'Cobaya de color blanco'.

Para la Caja 1:
· U₁ ≡ 'Caja 1'. Número total de Cobayas: 2+3 = 5 cobayas.

· P(B|U₁) = 3/5.
· P(M|U₁) = 2/5.

Para la Caja 2:
· U₂ ≡ 'Caja 2'. Número total de Cobayas: 4+2 = 6 cobayas.

· P(B|U₂) = 2/6 = 1/3.
· P(M|U₂) = 4/6 = 2/3.

Para la Caja 3:
· U₃ ≡ 'Caja 3'. Número total de Cobayas: 5+5 = 10 cobayas.

· P(B|U₃) = 5/10 = 1/2.
· P(M|U₃) = 5/10 = 1/2.

Las tres cajas tienen la misma probabilidad de ser escogidas:

· P(U₁) = 1/3.
· P(U₂) = 1/3.
· P(U₃) = 1/3.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de obtener una cobaya de color blanca, para ello, empleamos la Probabilidad Total:

P(B) = P(B|U₁)·P(U₁) + P(B|U₂)·P(U₂) + P(B|U₃)·P(U₃)

Sustituimos valores para obtener la solución a este apartado:

P(B) = (3/5)·(1/3) + (1/3)·(1/3) + (1/2)·(1/3) = 43/90

Por lo tanto, la probabilidad de obtener una cobaya blanca es de, aproximadamente 0.477778.


Apartado b)

En este apartado nos piden obtener la probabilidad de que dada que la cobaya sea blanca, sea de la primera caja:

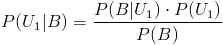
Sustituimos valores para obtener la solución a este apartado:

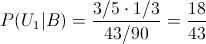
Por lo tanto, la probabilidad de que dada que la cobaya sea blanca, es de la urna primera es de, aproximadamente 0.418605.