Problema53: VAD

Ej53. Una solución contiene 2 tipos de virus A y B. En un mm³ de solución hay una media de 2 virus de tipo A y 4 virus de tipo B.

Obtener las siguientes probabilidades:

a) En 3 mm³ de solución haya más de 1 virus de tipo A.

b) En 4 mm³ de solución haya 5 virus de tipo B.

Realizamos una recopilación de datos del enunciado del problema:

· A ≡ 'Nº de virus del tipo A'.
· La variable aleatoria A sigue una distribución Poisson: X ~ P(2) por mm³.

· B ≡ 'Nº de virus del tipo B'.
· La variable aleatoria B sigue una distribución Poisson: X ~ P(4) por mm³.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en una solución de 3 mm³:

..2..--- 1
..λ..--- 3

Por lo tanto, el número medio de virus de tipo A en 3 mm3 de solución es:

· λ = (3·2)/1 = 6

La probabilidad que debemos obtener es la siguiente:

P(A > 1) = 1 - P(A ≤ 1) = 1 - [P(A = 0) + P(A = 1)]

Sustituimos valores para obtener la solución a este apartado:

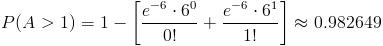
Por lo tanto, La probabilidad de que en 3 mm³ de solución, se encuentre más de 1 virus del tipo A es de, aproximadamente, 0.982649, es decir, es más que probable.


Apartado b)

Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en una solución de 4 mm³:

..4..--- 1
..λ..--- 4

Por lo tanto, el número medio de virus de tipo B en 4 mm³ de solución es:

· λ = (4·4)/1 = 16

La probabilidad que debemos obtener es la siguiente:

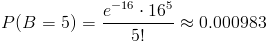
Por lo tanto, La probabilidad de que en 4 mm³ de solución, se encuentre cinco virus del tipo B es de, aproximadamente, 0.000983, es decir, es muy poco probable.