Problema61: VAC

Ej61. Un grupo de investigadores saben por propia experiencia que el diámetro de un determinado tipo de bacterias halladas en el análisis del agua de una charca sigue una distribución normal con varianza 9 mm².

También se sabe que el 69.5% de las bacterias analizadas tienen un diámetro inferior a 5.53 mm. Determinar:

a) ¿Cuál es el diámetro esperado de las bacterias?.

b) ¿Cuál es la probabilidad de encontrar bacterias con un diámetro superior a 4 mm?.


Sea la variable aleatoria X, diámetro de un determinado tipo de bacterias. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.

Por lo tanto: X ~ N(μ, 3) mm

Pasamos a resolver los distintos apartados del problema.


Apartado a)

En este problema, nos dan los datos de la probabilidad y debemos hallar el valor de la media de la variable aleatoria X que lo satisfaga.

Tenemos: P(X < . 5.53) = 0.695

Tipificamos:

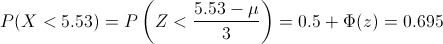
Despejamos:

Φ(z) = 0.695 - 0.5 = 0.195

Buscamos en las tablas de la Normal el valor 0.195, entonces: z = 0.51.

Por lo tanto, el diámetro esperado de las bacterias será de:

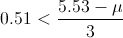
Despejamos μ y obtenemos la solución a este problema: μ = 4 mm.


Apartado b)

En este apartado, debemos obtener la siguiente probabilidad:

P(X > 4) = 1 - P(X ≤ 4)

Tipificamos:

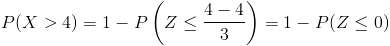
Operamos:

P(X > 4) = 1 - P(Z ≤ 0) = 1 - [0.5 + Φ(0)] = 1 - 0.5 = 0.5

Por lo tanto, la probabilidad de obtener bacterias con un diámetro mayor a 4 mm es de 0.5.