Problema43: Estimación y Pruebas de Hipótesis

Ej43. La nicotina contenida en 5 cigarrillos de cierta clase dio una media de 21.2 miligramos y una desviación típica de 2.05 miligramos.

Suponiendo que la distribución es normal, contrastar la hipótesis de que la nicotina media en esta clase de cigarrillos no excede de 19.7 miligramos al nivel α = 0.05.


Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Tamaño de la muestra: n = 5.
· Media muestral: x = 19.7.
· Desviación típica: σ = 2.05.
· Nivel de significación: α = 0.05.
· X ≡ 'Cantidad, mg, de nicotina en cigarrillo'.
· Sigue una distribución Normal: X~N(19.7, 2.05)

La prueba de hipótesis que plantea el enunciado del problema es:

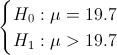
Es un contraste de media con desviación estándar conocida y el tamaño de la muestra menor que 30, el estadístico es:

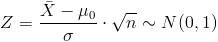
Obtenemos el valor del estadístico:

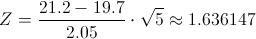
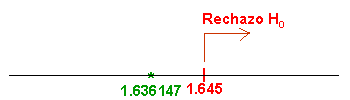
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≥ z_α

Para un nivel de significación de: α = 0.05, tenemos, en la tabla Normal:

· z_α = z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:

..1.64.............Z..........1.65
0.4495........0.45.....0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45

Calculamos:

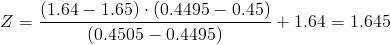
Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 1.636147 es menor que el valor de la región crítica, 1.645, por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que la cantidad media de nicotina no supera los 19.7 mg.


Ahora, obtendremos el p-valor, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen una región crítica, por lo tanto, tenemos una cola de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = P(Z > z) = P(Z > 1.636147) ≈ 1 - P(Z ≤ 1.64) = 1 - [0.5 + Φ(1.64)]

Operamos y buscamos en las tablas de la Normal:

p-valor = 0.5 - Φ(1.64) = 0.5 - 0.4495 = 0.0505

Al ser el nivel de significación del problema, α = 0.05, menor que el p-valor, aceptamos la hipótesis nula.

Cosa interesante es apreciar, que se acepta que el nivel medio de nicotina en cigarrillos es menor a 19.7 mg pero dicha aceptación, está casi al límite de ser rechazada.