Ej78. De los síntomas observados en un enfermo se deduce, por larga experiencia clínica, que puede tener la enfermedad A con probabilidad 0.5, la enfermedad B con 0.4 y la enfermedad C con 0.1.
Para precisar el diagnóstico se somete al paciente a una prueba que da resultado positivo en las personas que padecen las enfermedades A, B y C con probabilidades 0.3, 0.98 y 0.2 respectivamente.
Determinar:
a) Calcular la probabilidad de que la prueba de resultado positivo.
b) Si la prueba da resultado positivo, ¿cuál enfermedad es más probable que padezca el enfermo?.
Realizamos una recopilación de datos dados por el enunciado del problema:
· A ≡ 'Enfermedad A'.
· B ≡ 'Enfermedad B'.
· C ≡ 'Enfermedad C'.
· E ≡ 'Dar Positivo'.
· P(A) = 0.5.
· P(B) = 0.4.
· P(C) = 0.1.
· P(E|A) = 0.3.
· P(E|B) = 0.98.
· P(E|C) = 0.2.
Pasamos a resolver los apartados que nos propone el enunciado del problema.
Apartado a)
En este apartado nos piden obtener la probabilidad de dar positivo, para ello, empleamos la Probabilidad Total:
Sustituimos valores para obtener la solución a este apartado:
Por lo tanto, la probabilidad de dar positivo es de 0.562.
Apartado b)
En este apartado nos piden que en caso de que la prueba de positivo, cual de las enfermedades es la más probable que padezca el enfermo.
· Para la Enfermedad A:
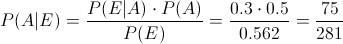
Por lo tanto, la probabilidad de que padezca la enfermedad A dado que de positivo es de, aproximadamente 0.266904.
· Para la Enfermedad B:
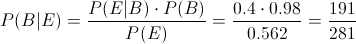
Por lo tanto, la probabilidad de que padezca la enfermedad B dado que de positivo es de, aproximadamente 0.697509.
· Para la Enfermedad C:
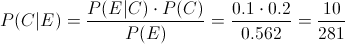
Por lo tanto, la probabilidad de que padezca la enfermedad C dado que de positivo es de, aproximadamente 0.035587.
Como solución a este apartado, el enfermo dado que de positivo, es más probable que padezca la enfermedad B.





0 comentarios:
Publicar un comentario