Problema60: VAC

Ej60. De una población de organismos suficientemente extensa se sabe que aproximadamente el 40% de sus individuos presenta un determinado polimorfismo que se manifiesta a través de un cierto fenotipo que se designa por k.

Se extrae una muestra aleatoria de tamaño 1000 y se desea conocer la probabilidad de que la muestra contenga más de 450 individuos de fenotipo k.


Realizamos una recopilación de datos que nos ofrece el enunciado:

· Sea la variable aleatoria X, número de individuos que presentan el fenotipo k.
· Tamaño de la muestra: N = 1000 individuos.
· La variable aleatoria discreta X sigue una distribución binomial: X ~ B(1000, 0.4)

Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:

1. n·p ≥ 5 → 1000·0.4 = 400 ≥ 5 OK.

2. n·q ≥ 5 → 1000·(1-0.4) = 600 ≥ 5 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

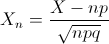
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(400, √240).

Debemos obtener la siguiente probabilidad:

P(X > 450)

Aplicamos el factor de corrección:

P(X > 450.5)

Y en estos momentos estamos en condiciones de tipificar por la Normal:

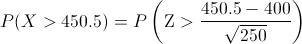
Aproximadamente es:

P(X > 450.5) ≈ P(Z > 3.26) = 1 - P(Z ≤ 3.26) = 1 - [0.5 + Φ(3.26)] = 0.5 - Φ(3.26)

Buscando en la tabla de la Normal, obtenemos la solución a este apartado:

P(X > 450.5) ≈ P(Z > 3.26) = 0.5 - Φ(3.26) = 0.5 - 0.4994 = 0.0006

Por lo tanto, la probabilidad de que en una muestra de tamaño 1000, contenga más de 450 individuos el fenotipo k, es de 0.0006, una probabilidad baja.