Ej44. Con el fin de estudiar el efecto de los rayos X sobre la viabilidad huevo-larva en “Tribolium castaneum” se irradiaron 1000 huevos de los que resultaron 572 larvas.
Hallar un intervalo de confianza para la proporción de larvas en huevos irradiados al nivel de confianza del 95%.
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del apartado:
· X ≡ 'Proporción de de larvas en huevos irradiados'.
· P(X) = 572/1000 = 143/250 = 0.572.
Nos pide realizar un intervalo de confianza de proporción, debemos verificar las siguientes condiciones:
· n = 1000 ≥ 30 OK.
· n·p = 1000·0.572 = 572 ≥ 5 OK.
· n·q = 1000·(1-0.572) = 428 ≥ 5 OK.
Por lo tanto, el intervalo de confianza a obtener es el siguiente:
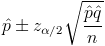
Para un 95%, obtenemos α:
100(1 - α) = 95
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:
· zα/2 = z0.05/2 = z0.025
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
0.5 - 0.025 = 0.475
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: z = 1.96.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la proporción de familias con coche al 95%, simplemente, sustituimos valores:
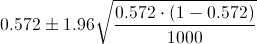
El intervalo de confianza es, aproximadamente:
[0.541333, 0.602667]
0 comentarios:
Publicar un comentario