Problema79: Probabilidad

Ej79. Tres cobayas A, B y C están siendo tratadas con tres tratamientos experimentales distintos, T₁, T₂, y T₃ respectivamente, para curar una enfermedad.

La probabilidad de curación con el T₁ es igual a 1/6, con el T₂ es igual a 1/4 y con el T₃ es igual a 1/3. Determinar:

a) Calcular la probabilidad de que exactamente una cobaya se cure.

b) Si solo una cobaya se cura, calcular la probabilidad de que sea la A.


Realizamos una recopilación de datos dados por el enunciado del problema:

· T₁ ≡ 'Curación del tratamiento experimental 1'.
· T₂ ≡ 'Curación del tratamiento experimental 2'.
· T₃ ≡ 'Curación del tratamiento experimental 3'.

· P(T₁) = 1/6.
· P(T₂) = 1/4.
· P(T₃) = 1/3.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de sólo se cure una de las tres cobayas:

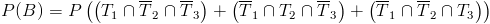
Para mayor facilidad, hemos denotado la probabilidad anterior como P(B) ya que así nos será más fácil su manejo y mención.

Sustituimos valores para obtener la solución a este apartado:

P(B) = 1/6·(1-1/4)·(1-1/3) + (1-1/6)·(1/4)·(1-1/3) + (1-1/6)·(1-1/4)·(1/3) = 31/72

Por lo tanto, la probabilidad de que se cure sólo una de las cobayas es de, aproximadamente 0.430556.


Apartado b)

En este apartado nos piden obtener la probabilidad de que al curarse sólo una de las cobayas, ésta sea la A:

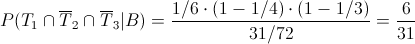
Por lo tanto, la probabilidad de que al curarse sólo una de las cobayas, ésta sea la A es de, aproximadamente 0.193548.