Problema55: VAD

Ej55. La probabilidad de que un enfermo reaccione desfavorablemente después de aplicarle un calmante es 0.01. Si dicho calmante se le aplica a 200 personas, determinar:

a) Media y desviación típica.

b) Probabilidad de que a lo sumo dos enfermos reaccionen desfavorablemente.

Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de enfermos que reaccionen desfavorablemente'.
· La variable aleatoria X sigue una distribución Binomial: X ~ B(200, 0.01).

Las características del tamaño de la muestra y la probabilidad relativamente baja que tiene, comprobaremos si podemos adaptar la distribución binomial a la de Poisson.

Para ello, debe cumplirse:

· n grande: n = 200 OK.

· n·p = 200·0.01 = 2 ≤ 7 OK.

Por lo tanto, se puede adaptar la variable aleatoria a la distribución de Poisson: X ~ P(2).

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

La media de una distribución de Poisson es el propio parámetro característico de dicha distribución:

· μ = λ = 2.

Y la desviación típica:

· σ = √ λ = √2 ≈ 1.414214.

Apartado b)

La probabilidad que debemos obtener es la siguiente:

P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

Sustituimos valores:

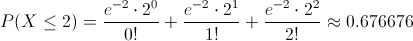
Por lo tanto, la probabilidad de que a lo sumo dos enfermos reaccionen desfavorablemente es de, aproximadamente, 0.676676.