Ej63. Una de las mayores contribuciones a la contaminación atmosférica es la provocada por los hidrocarburos procedentes de los tubos de escape de los automóviles. Sea X los gramos de hidrocarburo emitidos por un automóvil por cada dos kilómetros.
Supongamos que X es Normal con una media de 1 g. y una desviación típica de 0.25 g. Calcular las siguientes probabilidades:
a) Un automóvil emita más de 1.5 g.
b) Un automóvil emita menos de 1.2 g.
c) Un automóvil emita entre 1.3 y 1.4 g.
d) Un automóvil emita más de 0.65 g.
e) Un automóvil emita entre 0.4 y 0.7 g.
Sea la variable aleatoria X, gramos de hidrocarburos procedentes de los tubos de escape de automóviles cada 2 km. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Por lo tanto: X ~ N(1, 0.25) gramos cada 2 km.
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
En este apartado, debemos obtener la siguiente probabilidad:
P(X > 1.5) = 1 - P(X ≤ 1.5)
Tipificamos:
Obtenemos:
P(X > 1.5) = 1 - P(Z ≤ 2) = 1 - [0.5 + Φ(2)] = 0.5 - Φ(2)
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:
P(X > 1.5) = 0.5 - Φ(2) = 0.5 - 0.4772 = 0.0228
Por lo tanto, la probabilidad de que los gramos de hidrocarburos procedente de los tubos de escape de automóviles cada 2 km sea superior a 1.5 g, es de
0.0228.
Apartado b)
En este apartado, debemos obtener la siguiente probabilidad:
P(X <1.2)
Tipificamos:
Obtenemos:
P(X <1.2) = P(Z <0.8) = 0.5 + Φ(0.8)
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:
P(X <1.2) = 0.5 + 0.2881 = 0.7881
Por lo tanto, la probabilidad de que los gramos de hidrocarburos procedente de los tubos de escape de automóviles cada 2 km sea inferior a 1.2 g, es de 0.7881.
Apartado c)
En este apartado, debemos obtener la siguiente probabilidad:
P(1.3 ≤ X ≤ 1.4)
Tipificamos:
Obtenemos:
P(1.3 ≤ X ≤ 1.4) = P(1.2 ≤ Z ≤ 1.6) = [0.5 + Φ(1.6)] - [0.5 + Φ(1.2)] = Φ(1.6) - Φ(1.2)
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:
P(1.3 ≤ X ≤ 1.4) = P(1.2 ≤ Z ≤ 1.6) = Φ(1.6) - Φ(1.2) = 0.4452 - 0.3849 = 0.0603
Por lo tanto, la probabilidad de que los gramos de hidrocarburos procedente de los tubos de escape de automóviles cada 2 km esté comprendido entre 1.3 y 1.4 g, es de 0.0603.
Apartado d)
En este apartado, debemos obtener la siguiente probabilidad:
P(X > 0.65) = 1 - P(X ≤ 0.65)
Tipificamos:
Obtenemos:
P(X > 0.65) = 1 - P(Z ≤ -1.4) = 1 - P(Z ≥ 1.4) = 1 - [1 - P(Z <>
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:
P(X > 0.65) = 0.5 + Φ(1.4) = 0.5 + 0.4192 = 0.9192
Por lo tanto, la probabilidad de que los gramos de hidrocarburos procedente de los tubos de escape de automóviles cada 2 km sea superior a 0.65 g, es de 0.9192.
Apartado e)
En este apartado, debemos obtener la siguiente probabilidad:
P(0.4 ≤ X ≤ 0.7)
Tipificamos:
Obtenemos:
P(0.4 ≤ X ≤ 0.7) = P(-2.4 ≤ Z ≤ -1.2) = [1-(0.5 + Φ(1.2))] - [1-(0.5 + Φ(2.4))] = Φ(2.4) - Φ(1.2)
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:
P(0.4 ≤ X ≤ 0.7) = P(-2.4 ≤ Z ≤ -1.2) = Φ(2.4) - Φ(1.2) = 0.4918 - 0.3849 = 0.1069
Por lo tanto, la probabilidad de que los gramos de hidrocarburos procedente de los tubos de escape de automóviles cada 2 km esté comprendido entre 0.4 y 0.7 g, es de 0.1069.
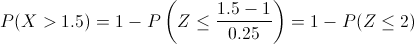
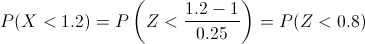
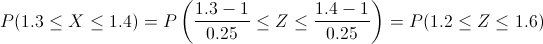
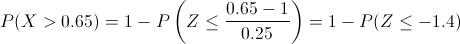
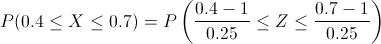





0 comentarios:
Publicar un comentario