Problema62: VAC

Ej62. Sea X la concentración en plomo en partes por millón en la corriente sanguínea de un individuo.

Supongamos que X es una variable Normal con media 0.25 y desviación típica 0.11. Una concentración superior o igual a 0.6 partes por millón se considera extremadamente alta.

¿Cuál es la probabilidad de que un individuo seleccionado aleatoriamente esté incluido en esta categoría?.


Sea la variable aleatoria X, concentración en plomo en ppm en la corriente sanguínea de un individuo. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.

Por lo tanto: X ~ N(0.25, 0.11) ppm.

En este problema, debemos obtener la probabilidad de que la concentración en plomo de un individuo sea extremadamente alta.

P(X ≥ 0.6) = 1 - P(X < 0.6)

Tipificamos:

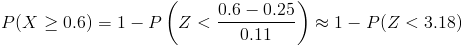
Obtenemos:

P(X ≥ 0.6) ≈ 1 - P(Z < 3.18) = 1 - [0.5 + Φ(3.18)] = 0.5 - Φ(3.18)

Buscando en la tabla de la Normal, obtenemos la solución a este apartado:

P(X ≥ 0.6) = 0.5 - Φ(3.18) = 0.5 - 0.4993 = 0.0007

Por lo tanto, la probabilidad de que un individuo contenga una cantidad extremadamente alta de plomo en la corriente sanguínea, es de 0.0007, una probabilidad baja.