Ej54. En un depósito de agua se ha detectado una concentración media de 0.25 bacterias nocivas por cada cm3 de agua.
Supuesto que las bacterias están aleatoriamente distribuidas, determinar:
a) ¿Cuál es la probabilidad de que en una extracción al azar de un volumen de 10 cm3 se encuentren al menos 3 bacterias nocivas?
b) Si la concentración fuera de 2 bacterias nocivas por cada 30 cm3 de agua, ¿cuál sería la probabilidad de que en una extracción al azar de un volumen de 10 cm3 se encontraran más de 3 bacterias nocivas?.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Nº de bacterias nocivas'.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(0.25) por cm3 de agua.
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en una solución de 10 cm3:
..0.25..--- 1
.....λ....--- 10
Por lo tanto, el número medio de bacterias en 10 cm3 de agua es:
· λ = (0.25·10)/1 = 2.5
La probabilidad que debemos obtener es la siguiente:
P(X ≥ 3) = 1 - P(X < .3) = 1 - [P(X = 0) + P(X = 1) + P(X = 2)]
Sustituimos valores para obtener la solución a este apartado:
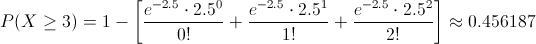
Por lo tanto, La probabilidad de que en 10 cm3 de solución, se encuentre al menos 3 bacterias es de, aproximadamente, 0.456187.
Apartado b)
En este apartado, nuestra variable aleatoria presenta un nuevo valor medio:
· X ~ P(2) por 30 cm3 de agua.
Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en una solución de 10 cm3:
..2..--- 30
..λ..--- 10
Por lo tanto, el número medio de bacterias en 10 cm3 de agua es:
· λ = (2·10)/30 = 2/3
La probabilidad que debemos obtener es la siguiente:
P(X > 3) = 1 - P(X ≤ 3) = 1 - [P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)]
Sustituimos valores:
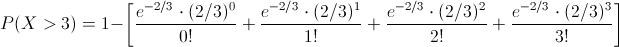
Operamos para obtener la solución a este apartado:
Por lo tanto, La probabilidad de que en 10 cm3 de solución, se encuentre más de 3 bacterias es de, aproximadamente, 0.004858.





2 comentarios:
Los pasos a seguir del ejercicio son los correctos , pero en cuestión al apartado A , la solución no se corresponde con lo que pide el enunciado , resuelve tal y como explica para que sea "de al menos 3" , pero en el enunciado te pide "menos de 3" , lo cual cambia la solución .
Buenas:
Tienes razón, es una errata del enunciado, lo que he hecho es actualizar el enunciado para que se resuelva con la premisa de al menos 3, así no hace falta actualizar las expresiones matemáticas.
Aún así, te pongo la solución a la premisa menos de 3:
· P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.543813.
Un saludo y muchas gracias por el apunte.
Publicar un comentario