Problema26: Estimación y Pruebas de Hipótesis

Ej26. En la fabricación de semiconductores, a menudo se utiliza una sustancia química para quitar el silicio de la parte trasera de las obleas antes de la metalización. En este proceso es importante la rapidez con la que actúa la sustancia.

Se han comparado dos soluciones químicas, utilizando para ello dos muestras aleatorias de 10 obleas para cada solución. La rapidez de acción observada es la siguiente (en mils/min):

Solución 1:	9,9..	9,4..	9,3..	9,6..	10,2..	10,6..	10,3..	10,0..	10,3..	10,1
Solución 2:	10.2	10.6	10.7	10.4	10.5	10.0	10.2	10.7	10.4	10.3

Determinar:

a) ¿Los datos apoyan la información que la rapidez promedio de acción es la misma para ambas soluciones? Para obtener sus conclusiones, utilice α = 0,05 y suponga que las varianzas de ambas poblaciones son iguales.

b) ¿Cuál es el valor P de esta prueba?.


En este problema, nos dan los datos de dos muestras aleatorias, por lo que tenemos que obtener la media de cada solución.

Para obtener la media:

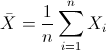
Por lo tanto:

· Solución 1:

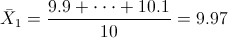
· Solución 2:

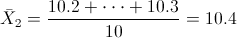
Para obtener la cuasi varianza:

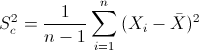
Por lo tanto, la cuasi varianza:

· Solución 1: S²_c1 = 1601/9000
· Solución 2: S²_c2 = 4/75

Pasamos a resolver los distintos apartados del problema.


Apartado a)

La prueba de hipótesis que plantea el enunciado del problema es:

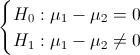
Es un contraste de diferencia de medias con desviación estándar desconocidas e iguales, el estadístico es:

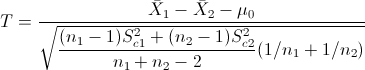
Obtenemos el valor del estadístico:

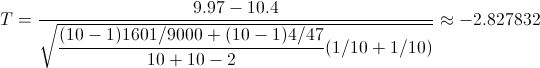
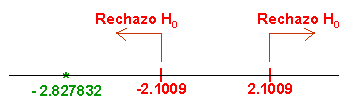
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

T ≤ - t_α/2,n1+n2-2, T ≥ t_α/2,n1+n2-2

Para un nivel de significación de: α = 0.05, tenemos, en la tabla t-Student:

· t_α/2,n1+n2-2 = t_{0.05/2,10+10-2}=t_0.025,18

Buscamos el valor en la tabla t-Student, y obtenemos: 2.1009.

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, -2.827832 está fuera del intervalo que compone la región crítica, (-2.1009, 2.1009), por lo tanto, rechazamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que la diferencia de medias son distintas, ya que se acepta la hipótesis alternativa.


Apartado b)

En este apartado, nos piden obtener el p-valor de la prueba del apartado anterior, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2 · P(T > |t|) = 2 · P(T > 2.827832)

Buscamos en las tablas de la t-Student, pero no encontramos el valor exacto para 2.827832 con 18 grados de libertad, por lo que podemos dar un intervalo donde se encuentre el p-valor:

En nuestro caso, el valor 2.827832 se encuentra comprendido entre los niveles de significancia:

0.005 < .T< .0.01

Como son áreas de cola, el p-valor estará comprendido entre los valores:

0.01 < .p-valor< .0.02

También, podemos dar un valor aproximado del p-valor mediante interpolación lineal:

..0.01...........T..............0.005
2.5524....2.827832....2.8784

De donde:

0.01 - 0.005.-> 2.5524 - 2.8784
0.01 - T.-> 2.5524 - 2.827832

Calculamos:

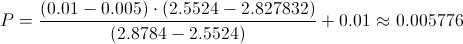
Sustituimos y obtenemos el p-valor:

p-valor = 2 · P(T > 2.827832) = 2·0.005776 = 0.011552

Como el p-valor es menor que el nivel de significación, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.