Ej59. Un grupo de investigadores está interesado en conocer la concentración media de una enzima en cierta población de algas. Se sabe por experiencias previas que la varianza de la concentración de esta enzima es de 35.
Si se obtiene una muestra de tamaño 15 dándonos un nivel de concentración media de 18 calcular un intervalo de confianza al nivel 95% (se supone normalidad).
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· X ≡ 'Concentración de una enzima en cierta población de algas'.
· Sigue una distribución Normal: X ~ N(18, √35).
· Tamaño de la muestra: n = 15.
En este problema nos pide realizar un intervalo de confianza para la media con varianza conocida y el tamaño de la muestra es menor que 30:
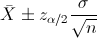
Para una confianza del 95%, obtenemos α:
100(1 - α) = 95
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:
· zα/2 = z0.05/2 = z0.025
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
0.5 - 0.025 = 0.475
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: 1.96.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:
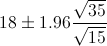
El intervalo de confianza bilateral al 95% es:
[15.006051, 20.993949]
0 comentarios:
Publicar un comentario