Problema60: Estimación y Pruebas de Hipótesis

Ej60. En un estudio de características corporales de las gaviotas de pico anillado, la variable considerada es la longitud del pico. Se dispone de los siguientes dato:

Hembra	..	Macho..
n1 = 51		n2 = 41
x1 = 59.1 mm		x2 = 62.5 mm
S1 = 1.9 mm		S2 = 2.0 mm

Determinar, utilizando α = 0.05, si hay evidencia para sostener el argumento de que la longitud media del pico de los machos sea mayor que la de las hembras.

NOTA: Siendo x₁ y x₂ las medias de la longitud del pico de las muestras dadas respectivamente.


En este problema nos dan los datos muestrales necesarios para obtener los resultados que nos piden.

Antes de estudiar si la longitud media del pico de los machos es mayor o no que el de las hembras, debemos saber si las varianzas son iguales o distintas.

La prueba de hipótesis de igualdad de varianzas:

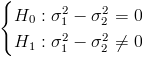
Es un contraste sobre igualdad de varianzas con medias desconocidas, el estadístico es:

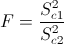
Obtenemos el valor del estadístico:

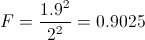
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

F ≤ f_{1-α/2,n1-1,n2-1}, F ≥ f_{α/2,n1-1,n2-1}

Para un nivel de significación de: α = 0.05, tenemos en la tabla distribución F:

· f_{1-α/2,n1-1,n2-1} = f_{1-0.05/2, 51-1, 41-1} = f_{0.975, 50, 40} = 1/f_{1-0.975,40,50} = 1/f_0.025,40,50

· f_{α/2,n1-1,n2-1} = f_{0.05/2, 51-1, 41-1} = f_0.025,50,40

Si buscamos en las tablas de la distribución F veremos que no se encuentra el valor exacto, para tal fin, aplicaremos interpolación lineal:

· Para el valor: f_0.025,40,50

..40.....50....60
1.88.....F.. .1.74

De donde:

40 - 60.-> 1.88 - 1.74
40 - 50 - Z.-> 1.88 - F

Calculamos:

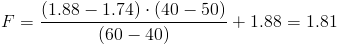
· Para el valor: f_0.025,50,40

..40.....50....60
1.88.....F.. .1.80

De donde:

40 - 60.-> 1.88 - 1.80
40 - 50 - Z.-> 1.88 - F

Calculamos:

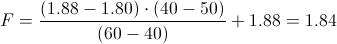
Por lo tanto, para un nivel de significación de: α = 0.05, tenemos:

· f_{0.975, 50, 40} = 1/f_0.025,40,50 ≈ 0.552486

· f_0.025,50,40 = 1.84

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 0.9025 está dentro del intervalo que compone la región crítica, (0.552486, 1.84), por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que las varianzas de ambas muestras, son iguales.

En estos momentos estamos en disposición de obtener las conclusiones que nos piden el problema.

Contraste sobre diferencias de medias con varianzas desconocidas e iguales:

Es un contraste de diferencia de medias con desviación estándar desconocidas e iguales y con tamaños muestrales de n₁ y n₂ ≥ 30 el estadístico es:

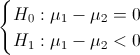
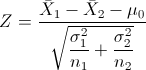
Obtenemos el valor del estadístico:

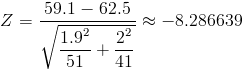
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ - z_α

Para un nivel de significación de: α = 0.05, El siguiente paso es obtener el valor de la z:

· z_α = z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.45, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..1.64...........Z..... ..1.65
0.4495.....0.45.. .0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z.-> 0.4495 - 0.45

Calculamos:

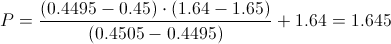
Realizamos una concepción gráfica de los datos hasta ahora obtenidos:

El valor del estadístico, -8.286639 se encuentra dentro de la región crítica, por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

Esto quiere decir que, existen evidencias significativas de que la longitud media de los picos machos son mayores que la de las hembras.