Problema58: Estimación y Pruebas de Hipótesis

Ej58. Una variable de interés en el estudio de la angina de pecho en las ratas es el consumo de oxígeno, medido en mililitros por minuto. El experimento proporcionó la siguiente información.

Placebo	..	FL113..
n1 = 9		n2 = 9
x1 = 1509 ml/min		x2 = 1702 ml/min
S1 = 169 ml/min		S2 = 181 ml/min

Determinar, utilizando α = 0.01:

a) Comprobar si hay diferencias en las varianzas poblacionales.

b) ¿Hay razón suficiente para pretender que el consumo de oxígeno de las ratas que toman FL113 sea más elevado que de las que toman placebo?

NOTA: Siendo x₁ y x₂ las medias del consumo de oxígeno de las muestras dadas respectivamente.


En este problema nos dan los datos muestrales necesarios para obtener los resultados que nos requieren.


Apartado a)

La prueba de hipótesis de igualdad de varianzas:

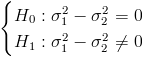
Es un contraste sobre igualdad de varianzas con medias desconocidas, el estadístico es:

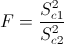
Obtenemos el valor del estadístico:

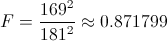
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

F ≤ f_{1-α/2,n1-1,n2-1}, F ≥ f_{α/2,n1-1,n2-1}

Para un nivel de significación de: α = 0.01, tenemos en la tabla distribución F:

· f_{1-α/2,n1-1,n2-1} = f_{1-0.01/2, 9-1, 9-1} = f_0.995,8,8 = 1/f_1-0.995,8,8 = 1/7.50 ≈ 0.133333

· f_{α/2,n1-1,n2-1} = f_{0.01/2, 9-1, 9-1} = f_0.005,8,8 = 7.50

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 0.871799 está dentro del intervalo que compone la región crítica, (0.133333, 7.50), por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que las varianzas de ambas muestras, son iguales.

Apartado b)

Contraste sobre diferencias de medias con varianzas desconocidas e iguales:

Es un contraste de diferencia de medias con desviación estándar desconocidas e iguales, el estadístico es:

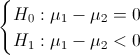
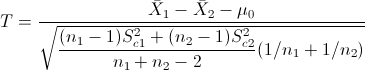
Obtenemos el valor del estadístico:

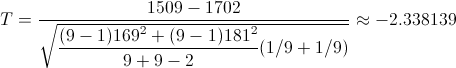
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

T ≤ - t_α,n1+n2-2

Para un nivel de significación de: α = 0.01, tenemos, en la tabla t-Student:

· t_α,n1+n2-2 = t_{0.01, 9+9-2} = t_{0.01, 16}

Buscamos el valor en la tabla t-Student, y obtenemos el valor: 2.5835.

Realizamos una concepción gráfica de los datos hasta ahora obtenidos:

El valor del estadístico, -2.338139 se encuentra fuera de la región crítica, por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que no existen diferencias en el consumo de oxígeno, por lo tanto, no hay razón para determinar que las ratas que toman FL113 consuman más oxígeno con respecto a las que toman placebo.