Problema46: Estimación y Pruebas de Hipótesis

Ej46. La siguiente tabla proporciona datos sobre la precipitación total registrada en 11 estaciones meteorológicas de dos provincias españolas:

Provincia A	100	89	84	120	130	105	60	70	90	108	130
Provincia B	120	115	96	115	140	120	75	90	108	130	135

Suponiendo independencia y normalidad, dar una estimación mediante un intervalo de confianza
al 80% para:

a) Cociente de varianzas de la pluviosidad entre las dos provincias.

b) Diferencia de las medias de la pluviosidad entre las dos provincias.

c) Diferencia de las medias de pluviosidad si se sabe por experiencia previa que la varianza de las precipitaciones en la provincia A es de 475 y en la provincia B de 350.


Recopilamos y obtenemos datos que nos serán de utilidad para posteriormente, resolver los distintos apartados.

Para obtener la media:

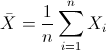
Por lo tanto:

·

·

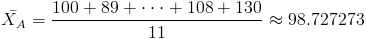
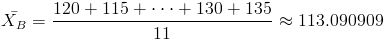
Para la cuasi desviación típica de cada muestra:

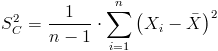
Para cada provincia, las desviaciones estándar son:

· S²_cA ≈ 524.818182

· S²_cB ≈ 389.490909

Para un 80%, obtenemos α:

100(1 - α) = 80

Despejamos el parámetro que nos interesa: α = 0.2.

En estos momentos, tenemos todos los elementos necesarios para resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

En este apartado nos piden obtener un intervalo de confianza al 80% para el cociente de varianzas con medias desconocidas:

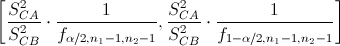
Para un nivel de significación de: α = 0.2, buscamos en tabla distribución F:

· f_{1-α/2,n1-1,n2-1} = f_{1-0.2/2,11-1,11-1} = f_0.9,10,10 = 1/f_1-0.9,10,10 = 1/f_0.1,10,10 = 1/2.32 ≈ 0.431034

· f_{α/2,n1-1,n2-1} = f_{0.2/2,11-1,11-1} = f_0.1,10,10 = 2.32

Sustituimos valores:

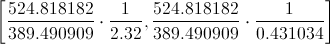
Por lo tanto, el intervalo de confianza es, aproximadamente:

[0.580795, 3.126080]

Apartado b)

En este apartado nos piden obtener un intervalo de confianza para la diferencia de medias de ambas provincias, pero nos encontramos con un problema, las varianzas son desconocidas de ambas muestras pero no sabemos si son iguales o no. Esto es importante ya que dependiendo de dicho matiz, cambia la forma de resolver el problema.

Por lo tanto, lo primero que debemos hacer, es una prueba de hipótesis para dictaminar si ambas varianzas desconocidas son iguales o no.

Tomo como hipótesis nula que ambas varianzas son iguales, siendo la hipótesis alternativa, que no lo son:

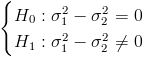
Cuyo estadístico es:

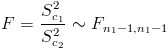
Ya disponemos de los datos necesarios para obtener el valor del estadístico:

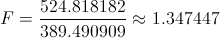
Para ver si aceptamos la hipótesis nula, debemos calcular la región crítica y evaluar los resultados obtenidos. La región crítica para este estudio es:

F ≥ F_{α/2,n1-1,n2-1} , F ≤ F_{1-α/2, n1-1,n2}-1

Para un nivel de significación de: α = 0.2, buscamos en tabla distribución F:

· f_{1-α/2,n1-1,n2-1} = f_{1-0.2/2,11-1,11-1} = f_0.9,10,10 = 1/f_1-0.9,10,10 = 1/f_0.1,10,10 = 1/2.32 ≈ 0.431034

· f_{α/2,n1-1,n2-1} = f_{0.2/2,11-1,11-1} = f_0.1,10,10 = 2.32

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 1.347447 está dentro de la marcada por la región crítica, [0.431034, 2.32], por lo tanto, aceptamos la hipótesis nula.

Una vez que sabemos que la varianza de ambas muestras son iguales, pasamos a confeccionar el intervalo de confianza para la diferencia de medias.

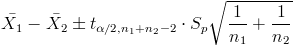
El siguiente paso es obtener los valores de:

· t_α/2,n1+n2-2 = t_{0.2/2,11+11-2}=t_0.1,20

Buscamos el valor en la tabla t-Student, y obtenemos: 1.3253.

Necesitamos obtener el valor de Sp:

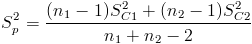
Sustituimos valores:

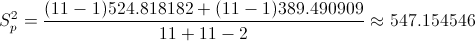
Ya disponemos todos los datos necesarios para obtener el intervalo bilateral de confianza al 80% de la diferencia de medias con varianzas desconocidas e iguales:

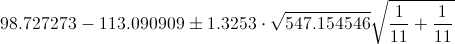
El intervalo de confianza bilateral al 80% es:

[-27.582309, -1.144963]

Apartado c)

En este apartado nos pide realizar un intervalo de confianza para la diferencia entre las medias con varianzas conocidas:

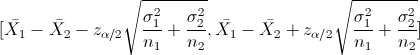
El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.2/2 = z_0.1

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.1 = 0.4

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.4, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..1.28...........Z..... ..1.29
0.3997.....0.4.. .0.4015

De donde:

1.28 - 1.29.-> 0.3997 - 0.4015
1.28 - Z.-> 0.3997 - 0.4

Calculamos:

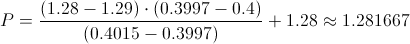
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 80%, simplemente, sustituimos valores:

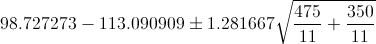
El intervalo de confianza bilateral al 80% es, aproximadamente:

[-25.463198, -3.264074]