Problema47: Estimación y Pruebas de Hipótesis

Ej47. En una fábrica de productos estéticos, se analiza el contenido en los tubos de una determinada crema hidratante. Se toman 10 tubos y se determina el contenido en gramos de crema de cada uno de ellos, obteniendo los siguientes resultados: :

Tubo	1	2	.3.	4	5	6	7	8	9	10
Contenido	5.2	4.9	5	5.1	5.2	4.8	4.9	5.3	4.6	5.4

Por otras muchas determinaciones se sabe que la desviación típica de la población es de 0.10 gramos y queremos averiguar si los valores anteriores son compatibles con la media de 5 gramos para la población, supuesta esta normal a un nivel de significación del 0.05.


Recopilamos y obtenemos datos que nos serán de utilidad.

Para obtener la media:

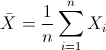
Por lo tanto:

·

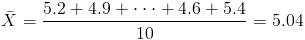
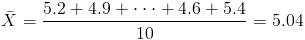
Nos piden realizar una prueba de hipótesis de que el contenido medio es de 5 gramos con varianza conocida:

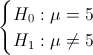
Cuyo estadístico es:

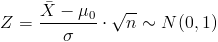
Sustituimos valores y obtenemos el valor del estadístico:

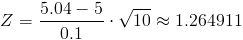
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ - z_α/2 , Z ≥ z_α/2

Para un nivel de significación de: α = 0.05, tenemos:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es 1.96.

Comprobamos el valor del estadístico con la región crítica:

No se cumplen las condiciones de la región crítica, por lo tanto, aceptamos la hipótesis nula.

Esto indica que existen evidencias significativas de que la cantidad media de crema en los tubos es de 5 gramos.

Para refutar el estudio realizado anteriormente, vamos a obtener el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2·P(Z > |z|) = 2·P(Z > 1.264911) ≈ 2·[1 - P(Z ≤ 1.26)] = 2·[1 - (0.5 + Φ(1.26))] = 2·[0.5 - Φ(1.26)]

Buscamos en las tablas de la Normal el valor tipificado de 1.26, el cual es 0.3962.

Sustituimos y obtenemos el p-valor:

p-valor = 2·[0.5 - Φ(1.26)] = 2·[0.5 - 0.3962] = 0.2076

Como el p-valor es mayor que el nivel de significación, aceptamos la hipótesis nula, se cumple el anterior razonamiento mediante la región crítica.