Ej66. La media de las temperaturas obtenidas en una región durante un año es de 25ºC y la desviación típica de 10ºC.
Si las temperaturas obedecen a una ley normal, calcular la probabilidad de que en un día elegido al azar la temperatura esté comprendida entre 20 y 30 grados.
Sea la variable aleatoria X, temperatura en una región durante un año. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Por lo tanto: X ~ N(25, 10) ºC.
En este problema, debemos obtener la probabilidad de que la temperatura esté comprendida entre los valores 20 y 30 ºC:
P(20 ≤ X ≤ 30)
Tipificamos:
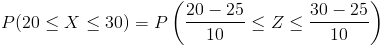
Operamos:
P(20 ≤ X ≤ 30) = P(-0.5 ≤ Z ≤ 0.5) = (0.5 + Φ(0.5)) - [1 - (0.5 + Φ(0.5))]
Despejamos y buscamos en la tabla de la Normal:
P(20 ≤ X ≤ 30) = P(-0.5 ≤ Z ≤ 0.5) = Φ(0.5) + Φ(0.5) = 2·Φ(0.5) = 2·0.1915 = 0.383
Por lo tanto, la probabilidad de que la temperatura esté comprendida entre 20 y 30 ºC en una región es de 0.383.





1 comentarios:
Hola.
quiero saber si me podrías ayudar con una gran duda que tengo. Me proponen este ejercicio estadístico y no lo he podido resolver hasta el día de hoy.
Se conoce la función de densidad f(x)= c(4+6x-3x^2) para 01)
d) P(x1.9)
Si me puedes ayudar te estaré eternamente agradecida desde Ecuador.
Publicar un comentario