Ej32. El Ministerio de la Vivienda desea conocer el número de garajes que es deseable construir, a fin de que sus moradores puedan aparcar allí sus vehículos.
Determinar:
a) Se entrevista a 3238 familias. Entre ellas hay 971 que poseen coche. A partir de esta muestra, obtener un intervalo de confianza de la proporción p de familias que tienen coche con un nivel de confianza del 95%.
b) Determinar el número de familias a entrevistar para estimar la proporción p de familias que tienen coche con un error inferior a 0.05 y un nivel de confianza del 95%.
Apartado a)
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del apartado:
· X ≡ 'Proporción de familias con coche'.
· P(X) = 971/3238.
Nos pide realizar un intervalo de confianza de proporción, debemos verificar las siguientes condiciones:
· n = 3238 ≥ 30 OK.
· n·p = 3238·(971/3238) = 971 ≥ 5 OK.
· n·p·q = 3238·(971/3238)·(1-971/3238) ≈ 679.8 ≥ 5 OK.
Por lo tanto, el intervalo de confianza a obtener es el siguiente:
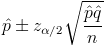
Para un 95%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:
· zα/2 = z0.05/2 = z0.025
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: z = 1.96.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la proporción de familias con coche al 95%, simplemente, sustituimos valores:
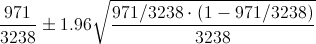
Apartado b)
En este apartado, debemos obtener el valor del parámetro n dado un error, para ello, empleamos la expresión del error y despejamos el parámetro pedido.
La expresión del error se muestra a continuación:
Operamos y despejamos el parámetro n:
Como el parámetro n representa al número de familias que se deben entrevistar para estimar la proporción de familias que tienen coche con un error inferior a 0.05 y un nivel de confianza del 95%, debe ser un número entero positivo.
Por lo tanto, n = 323 familias.


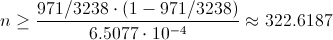




0 comentarios:
Publicar un comentario