Problema37: VAC

Ej37. La Comisaría del Plan de Desarrollo mantiene que tres de cada cinco españoles poseerán coche dentro de diez años.

¿Cuántos garajes serán necesarios construir para un edificio residencial de 423 apartamentos, para satisfacer la demanda con al menos un 95% de probabilidad?.


Sea la variable aleatoria discreta X, número de garajes que son necesarios construir para cierto edificio residencial. Realizamos en resumen de los datos que nos ofrece el enunciado del problema:

La variable aleatoria discreta X, sigue una distribución binomial: X ~ B(423, 3/5).

Comprobaremos, si se puede aproximar a la normal, para ello, se deben cumplir las siguientes condiciones:

1. n·p ≥ 5 → 423·3/5 = 253.8 ≥ 5 OK.

2. n·q ≥ 5 → 423·(1-3/5) = 169.2 ≥ 5 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

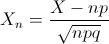
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(253.8, √(101.52)).

Debemos calcular: P(X ≤ n) ≥ 0.95, es decir, el valor del número de garajes necesarios para que se cumpla dicha probabilidad.

Tipificamos:

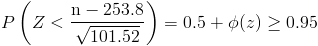
Despejamos Φ(z):

Φ(z) = 0.95 - 0.5 = 0.45

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.45, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:

..1.64...........Z..... ..1.65
0.4495.....0.450.. .0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z.-> 0.4495 - 0.450

Calculamos:

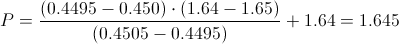
Por lo tanto, tenemos:

Despejamos el parámetro n, número de garajes necesarios a construir en el edificio residencial dado en el problema: n ≥ 270.374549.

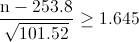
Pero en número de garajes a construir debe ser un número entero positivo, por lo tanto, la solución a este problema es: n ≥ 271 garajes a construir.