Problema26: VAC

Ej26. En un hospital, el número medio de pacientes con dolor abdominal atendidos por día es 26.

Calcular la probabilidad de que un día determinado haya más de 35 pacientes con dolor abdominal.

NOTA: Considérese la distribución de Poisson.


Sea la variable aleatoria X, número de pacientes con dolor abdominal. El enunciado nos sugiere que la variable aleatoria sigue una distribución de Poisson: X ~ P(26).

Comprobaremos, si se puede aproximar a la normal, para ello, se debe cumplir la siguiente condición:

1. λ = 26 > 25 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

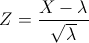
Por lo tanto: X ~ N(26, √26).

Debemos calcular: P(X > 35), operamos la desigualdad: 1 - P(X ≤ 35), aplicamos la corrección por continuidad: 1 - P(X ≤ 35.5).

Tipificamos:

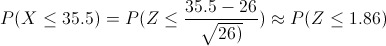
Así qué:

P(X > 35.5) ≈ 1 - P(Z ≤ 1.86) = 1 - (0.5 + Φ(1.86))

Buscamos el valor en las tablas y sustituyendo valores, obtenemos la solución a este problema:

P(X > 35.5) ≈ 0.5 - Φ(1.86) = 0.5 - 0.4686 = 0.0314