Ej25. Una encuesta reciente reveló que, de 2013 adultos elegidos al azar, 1358 (o el 67.5%) afirmaron ser usuarios de Internet (según datos del Pew Research Center).
Si la proporción de todos los adultos que utilizan Internet es en realidad de 2/3. Calcular la probabilidad de que una muestra aleatoria de 2013 adultos produzca exactamente 1358 usuarios en Internet.
Sea la variable aleatoria X, adultos usuarios de Internet. El número total de usuarios de Internet es: 2013.
A parte, nos indica el enunciado, que la probabilidad de todos los adultos usuarios de Internet es de 2/3.
Estos datos, nos hace preveer que estamos ante ejemplo de acierto o error, en este caso, el acierto es encontrar x usuarios de Internet, por lo que estamos ante una distribución binomial: X ~ B(2013, 2/3).
Comprobaremos, si se puede aproximar a la normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5: 2013 · 2/3 = 1342 ≥ 5 OK.
2. n·q ≥ 5: 2013 · (1 - 2/3) = 671 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
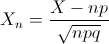
Por lo tanto: X ~
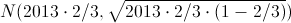 .
.Debemos calcular: P(X = 1358), aplicamos la corrección por continuidad: P(1357.5 ≤ X ≤ 1358.5).
Tipificamos:
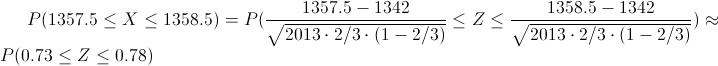
Así qué:
Buscamos el valor en las tablas y sustituyendo valores, obtenemos la solución a este problema:





4 comentarios:
No consigo diferencias los problemas de binomial de las distribuciones discretas con los de las distribuciones continuas¿Podrá aclararmelo?
Gracias.
Buenas:
La diferencia es básica y clara. Piensa en modo matemático.
· Distribuciones Discretas: Son aquellas que precisan de una probabilidad determinada o de eventos únicos. Por ejemplo, la probabilidad del evento 5, o la probabilidad de los eventos del 1 al 5 (Sería la suma de probabilidades de los eventos 1 al 5).
· Distribuciones Continuas: Se basan en el área que encierra sus eventos. Por ejemplo, para una distribución continua, la probabilidad de un evento determinado, por ejemplo el 5, es justamente cero (ya que para un elemento infinitesimal, no existe área).
En este caso (en este problema), la variable aleatoria sigue una distribución claramente discreta (y binomial), pero al cumplirse los requisitos (normalmente cuando el número de eventos es muy grande), se puede aproximar a una variable aleatoria continua de manera fiable.
¿Y por qué se aproxima a una distribución continua? Pues porque es relativamente más cómodo resolver un área que muchos elementos separados.
Un saludo y gracias por tu comentario.
Vale,hasta ahí todo claro,pero...como los diferencio en los enunciados cuando va a ser cero la probabilidad de un evento y cuando no?
Gracias.
Buenas:
Eso es con la práctica cómo normalmente vamos adquiriendo la destreza de diferencias de que tipología y tipo son las variables aleatorias.
Aún así, las variables aleatorias continuas se suelen indicar. Ya sea por que te digan que sigue una determinada distribución o por la configuración y datos que te ofrece el enunciado hace que encaje en una de las distribuciones que hayas estudiado.
Un saludo.
Publicar un comentario