Problema66: Estimación y Pruebas de Hipótesis

Ej66. Se quiere comprobar la efectividad de una vacuna contra una enfermedad. Para ello se suministró la vacuna a 100 animales y se les comparó con un grupo testigo de otros 100.

A los 200 se les contagió la enfermedad. Entre los vacunados murieron 8 como resultado de la enfermedad y del grupo testigo hubo 20 muertos.

¿Podemos concluir que la vacuna es eficaz en reducir la tasa de mortalidad?

NOTA: Suponer normalidad con α = 0.05.


Realizamos una recopilación de datos que nos ofrece el enunciado del problema.

● Vacunados:

· ṗ₁ = 8/100 = 0.08.
· n₁ = 100.

● Grupo Testigo:

· ṗ₂ = 20/100 = 0.2.
· n₂ = 100.

Debemos realizar un contraste sobre diferencia de proporciones, pero para ello, se deben cumplir las siguientes condiciones:

· n₁·ṗ₁ = 100·0.08 = 8 ≥ 5...OK
· n₁·(1 - ṗ₁) = 100·(1 - 0.08) = 92 ≥ 5...OK

· n₂·ṗ₂ = 100·0.2 = 20 ≥ 5...OK
· n₂·(1 - ṗ₂) = 100·(1 - 0.2) = 80 ≥ 5...OK

· n₁ = 100 ≥ 30.. OK
· n₂ = 100 ≥ 30...OK

Se cumplen todos los requisitos.

Prueba de hipótesis sobre diferencia de proporciones:

El estadístico es:

Obtenemos el valor del estadístico:

Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ -z_α

Para un nivel de significación de: α = 0.05, tenemos, en la tabla Normal:

· z_α = z_0.05

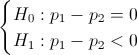
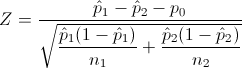
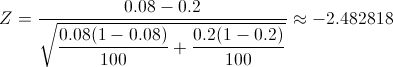
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:

..1.64.............Z..........1.65
0.4495........0.45.....0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45

Calculamos:

Realizamos una concepción gráfica de los datos hasta ahora obtenidos:

El valor del estadístico, -2.482818 se encuentra dentro de la región crítica -1.645, por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

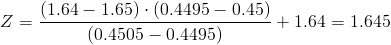
Esto quiere decir que, existen evidencias significativas de que la proporción de supervivencia en animales vacunados es mayor que en el grupo testigo.

Por lo tanto, podemos determinar que la vacuna es efectiva.