 | You also can read this text in English! Problem82: Hypothesis Test |
Ej82. Una marca de refrescos de cola, dice que sus latas contienen 33 cl de refresco. Para comprobarlo se escogen aleatoriamente 50 latas. La media fue de 32 cl y la desviación típica muestral de 2 cl.
Si se asume que el estudio sigue una distribución normal, ¿se puede decir, con un nivel de confianza del 95%, que están engañando a los consumidores?
Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:
· Tamaño de la muestra: n = 50.
· Media muestral: x = 32.
· Desviación típica muestral: Sc = 2.
· X ≡ 'Contenido, cl, de refresco en una lata'.
· Sigue una distribución Normal: X ~ N(32, 2)
La prueba de hipótesis que plantea el enunciado del problema es:
Es un contraste de media con desviación estándar desconocida y el tamaño de la muestra mayor que 30, el estadístico es:
Obtenemos el valor del estadístico:
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
Z ≤ - zα
Obtenemos el parámetro α: 100(1 - α) = 95, despejamos: α = 0.05.
· zα = z0.05
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
0.5 - 0.05 = 0.45
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..1.64.............Z..........1.65
0.4495........0.45.....0.4505
De donde:
1.64 - 1.65.---> 0.4495 - 0.4505
1.64 - Z..---> 0.4495 - 0.45
Calculamos:
Comprobamos el valor del estadístico con la región crítica:
El valor del estadístico, -3.535534 es menor que el valor de la región crítica, -1.645, por lo tanto, rechazamos la hipótesis nula y aceptamos la Hipótesis alternativa.
Esto quiere decir que, existen evidencias significativas de que la cantidad media de refresco en las latas es inferior a 33 cl, en otras palabras, la marca de refrescos de cola están engañando a los consumidores.
Ahora, obtendremos el p-valor, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen una región crítica, por lo tanto, tenemos una cola de probabilidad, el p-valor en estas condiciones, se calcula cómo:
p-valor = P(Z >|z|) = P(Z > |-3.535534|) ≈ 1 - P(Z ≤ 3.54) = 1 - [0.5 + Φ(3.54)]
Operamos y buscamos en las tablas de la Normal:
p-valor = 0.5 - Φ(3.54) = 0.5 - 0.4998 = 0.0002
Al ser el nivel de significación del problema, α = 0.05, mayor que el p-valor, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.
Queda demostrado por ambos métodos de que la marca de refrescos miente al consumidor.

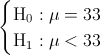
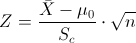
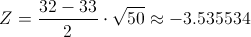
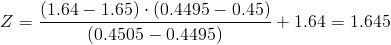
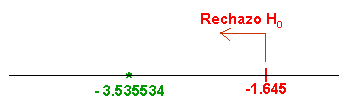




0 comentarios:
Publicar un comentario