 | ¡Puedes leer este texto en español! Problema82: Puebas de Hipótesis |
Ej82. A soft drink company says that its soft drink cans contain 33 cl. To know if it's true, 50 cans are selected randomly. The sample mean was 32 cl and the sample standard deviation was 2 cl.
If the studio follows a Normal distribution, Can we say that they are lying to consumers at the 95% confidence level?
We perform a data compilation given by problem statement:
· Sample size: n = 50.
· Sample mean: x = 32.
· Sample standard deviation: Sc = 2.
· X ≡ 'Content of soft drink cans in cl'.
· The random variate X follows a Normal distribution: X ~ N(32, 2)
The Hypothesis Test given by the problem statement is:
It's a Hypothesis Test to test the mean with unknown standard variation and the sample size is greater than 30, the statistical is:
We obtain the statistical value:
To check if we accept or reject the Null Hypothesis, we'll use the method of critical region:
Z ≤ - zα
We get the α-parameter: 100(1 - α) = 95, we solve: α = 0.05.
· zα = z0.05
Considering the characteristics of Aqueronte's tables, we must adapt that value:
0.5 - 0.05 = 0.45
In this case, it isn't the exact value so, we make a linear interpolation:
..1.64.............Z..........1.65
0.4495........0.45.....0.4505
Where:
1.64 - 1.65.--> 0.4495 - 0.4505
1.64 - Z..--> 0.4495 - 0.45
We calculate:
We check the statistical value with the critical region:
The statistical value, -3.535534 is less than the critical region value, -1.645, so we reject the Null Hypothesis and we accept the Alternative Hypothesis.
This means, there are enough evidences that the content of soft drink cans is less than 33 cl, in other words, the soft drink company is lying to consumers.
Now, let's get the p-value of test to corroborate the previous study. In our case, there is a one-tailed test then, the p-value is calculated as:
p-value = P(Z >|z|) = P(Z > |-3.535534|) ≈ 1 - P(Z ≤ 3.54) = 1 - [0.5 + Φ(3.54)]
We calculate and we search the value in Normal table:
p-value = 0.5 - Φ(3.54) = 0.5 - 0.4998 = 0.0002
As the level of significance, α = 0.05, is greater than the p-value then, we reject the Null Hypothesis and we accept the Alternative Hypothesis.
So, it's demonstrated that the soft drink company is lying to consumers by both methods.


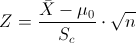

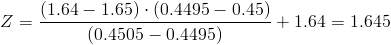
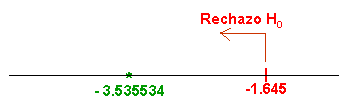




0 comentarios:
Publicar un comentario