 | You also can read this text in English! Problem92: Probability |
Ej92. Un profesor con bastantes años de experiencia ha observado que el 60% de los alumnos que suspenden un examen de una asignatura acuden a la revisión de exámenes, mientras que de entre los que obtienen la calificación de aprobado, los que acuden a la revisión son un 5% y de entre los que obtienen notable o más acuden un 10%.
En el examen cuya revisión acaba de terminar, hubo un 40% de suspensos, un 50% de aprobados y un 10% de exámenes calificados como notable o más.
Calcular la probabilidad de que un examen que se ha revisado estuviera calificado como suspenso.
Realizamos una recopilación de datos dados por el enunciado del problema:
· S ≡ 'Alumnos suspenden el examen'.
· A ≡ 'Alumnos de nota aprobado'.
· X ≡ 'Alumnos de nota notable o más'.
· P(S) = 0.4.
· P(A) = 0.5.
· P(X) = 0.1.
· R ≡ 'Alumnos van a revisión'.
· P(R|S) = 0.6.
· P(R|A) = 0.05.
· P(R|X) = 0.1.
Nos piden obtener la probabilidad de que dado que un examen haya sido revisado, éste esté calificado como suspenso, emplearemos para tal fin la Ley de Bayes:
Pero antes, debemos obtener previamente, la probabilidad del evento R (Alumnos van a revisión), para tal fin, emplearemos la Ley de la Probabilidad Total:
P(R) = P(R|S)·P(S) + P(R|A)·P(A) + P(R|X)·P(X)
Sustituimos valores para obtener la probabilidad de dicho evento:
P(R) = P(R|S)·P(S) + P(R|A)·P(A) + P(R|X)·P(X) = 0.6·0.4 + 0.05·0.5 + 0.1·0.1 = 0.275
En estos momentos, ya estamos en disposición de dar la solución al presente problema:
Por lo tanto, la probabilidad de que dado que un examen haya sido revisado, éste esté calificado como suspenso es de, aproximadamente 0.872727.

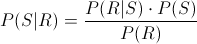
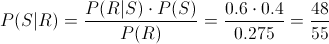




0 comentarios:
Publicar un comentario