 | ¡Puedes leer este texto en español! Problema92: Probabilidad |
Ej92. A teacher with too many years of experience has seen that the 60% of students who don't pass a determinated exam going to review the exam while the students with passing grades going to review the exam a 5% and finally, the students with notable (or more) grades are a 10% who going to review the exam.
In the exam whose has review just finished, there were a 40% of suspended, a 50% of passing grades and lastly a 10% of notable (or more) grades.
Calculate the probability that an exam which has been reviewed, this was qualified as suspended.
We perform a data compilation given by the problem statement:
· S ≡ 'Students who have suspended the exam'.
· A ≡ 'Students who have passing grades'.
· X ≡ 'Students who have notable (or more) grades'.
· P(S) = 0.4.
· P(A) = 0.5.
· P(X) = 0.1.
· R ≡ 'Students who going to review the exam'.
· P(R|S) = 0.6.
· P(R|A) = 0.05.
· P(R|X) = 0.1.
We are asked to obtain that an exam which has been reviewed, it was qualified as suspended, we need to apply the Bayes's Theorem for this purpose:
But before, we must obtain the probability of R event (Students who going to review the exam), therefore, we use the Total Probability law:
P(R) = P(R|S)·P(S) + P(R|A)·P(A) + P(R|X)·P(X)
We replace for the numerical values to get the probability of that event:
P(R) = P(R|S)·P(S) + P(R|A)·P(A) + P(R|X)·P(X) = 0.6·0.4 + 0.05·0.5 + 0.1·0.1 = 0.275
At present, we can provide the solution to this problem:
So, the probability that an exam which has been reviewed, this was qualified as suspended is, aproximately 0.872727.

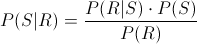
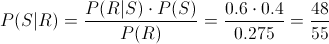




0 comentarios:
Publicar un comentario