Problema31: Estimación y Pruebas de Hipótesis

Ej31. Una empresa le propone al director de una fábrica mejoras en su planta de fabricación. Un nuevo método que, supuestamente, reduce el tiempo empleado en el montaje de uno de sus productos.

Con el propósito de comparar tal método con el empleado habitualmente, se selecciona aleatoriamente a siete de sus empleados para que llevasen a cabo el montaje con los dos sistemas y anotaran los tiempos empleados en el montaje, obteniendo los siguientes resultados

Trabajador	1	2	3	4	5	6	7
Método Habitual	38.	32.	41.	35.	42.	32.	45.
Método Nuevo	30	32	34	37	35	26	38

Supuesto que el tiempo de montaje sigue una distribución Normal, hallar un intervalo de confianza para la diferencia de los tiempos medios de montaje, al 95%.

NOTA: Considerar las muestras pareadas.


Debemos restar los datos de las muestras dadas una a una, obteniéndose la siguiente tabla:

Trabajador	1	2	3	4	5	6	7
Diferencia	8	0	7	-2	.7	.6	7

Calculamos los datos estadísticos básicos.

Para obtener la media:

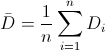
Por lo tanto:

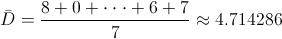
Para obtener la cuasi varianza:

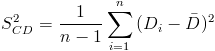
Por lo tanto, la cuasi desviación estándar:

S_CD ≈ 3.988077

En este problema nos pide realizar un intervalo de confianza para la diferencia de medias con varianza desconocida y tamaño de la muestra es menor que 30:

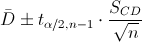
Para una confianza del 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener los valores de:

· t_α/2,n-1 = t_0.05/2,7-1=t_0.025,6

Buscamos el valor en la tabla t-Student, y obtenemos: 2.4469.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la diferencia de tiempos empleados con un 95%, simplemente, sustituimos valores:

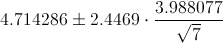
El intervalo de confianza bilateral al 95% es:

[1.025948, 8.402624]