Ej32. El propietario de un establecimiento, observa que los ingresos medios por cliente que acude a comprar son de 20 euros, con una desviación típica de 5 euros, suponiendo la independencia de los ingresos de sus clientes, calcular:
a) ¿Cuántos clientes tienen que acudir al establecimiento un día cualquiera para que, con una probabilidad de 0.9772, los ingresos al final del día sean superiores a 1000 euros?.
b) El propietario selecciona al azar 36 clientes del establecimiento. ¿Cuál es la probabilidad de que los ingresos totales que dejan los 36 clientes del establecimiento superen los 750 euros?.
Emplearemos la distribución normal para hallar los apartados requeridos.
Cuya media por cliente es: 20 y la desviación estándar por cliente: 5.
En este problema, la clave radica en que los datos ofrecidos están por clientes, mientras que los cálculos totales deberemos considerar a todos ellos, por lo tanto, tendremos:
· Media ≡ μ = 20·n
· Desviación estándar ≡ σ = 5√n
Sea la variable aleatoria X, ingreso de los clientes. Dicha variable continua aleatoria, sigue una distribución Normal: X ~ N(20n, 5√n)
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
Tenemos que resolver:
Operamos:
Tipificamos a la Normal:
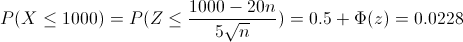
Despejamos:
Nos da un valor negativo, ésto indica que el valor de z se encuentra en la parte izquierda de la campana de Gauss. Las tablas que dispone Aqueronte, no ofrecen los valores negativos de la curva, pero no hay problema ya que son simétricos, por lo que buscamos en la tabla el valor 0.4772 que de un z válido.
En la tabla, encontramos el valor exacto: z = 2.00, ahora bien, tenemos que tener en cuenta que la z válida está en el semieje negativo X: z = -2.00.
Por lo tanto, el número de clientes serán:
Despejamos:
Simplificamos:
Operamos la desigualdad:
Despejamos:
Resolviendo la ecuación cuadrática, obtenemos dos posibles soluciones para n:
· n1 ≈ 53.662743
· n2 ≈ 46.587257
¿Cuál de las dos soluciones es válida? En nuestro caso será n1 (~53.662743), ya que es la solución que cumple con todos los pasos que hemos realizado anteriormente en este apartado hasta llegar a la solución.
¿Y por qué tenemos dos soluciones? Pues ya se ha comentado anteriormente algo, es simplemente porque la curva de la Normal es simétrica, esto hace que tengamos dos soluciones: una en su parte derecha y otra en su parte izquierda.
Por lo tanto, n debe ser un valor entero positivo, n > 53.
Apartado b)
En este apartado debemos obtener la siguiente probabilidad:
Teniendo en cuenta el valor obtenido de n en el primer apartado, la variable continua aleatoria, sigue una distribución Normal: X ~ N(20·36, 5√36).
Tipifico a la Normal:
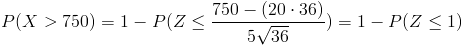
Por lo tanto, tenemos:
Buscamos en la tabla de la Normal dicho valor y resolvemos este apartado:
Por lo tanto, la probabilidad de que los ingresos totales que dejen los 36 clientes del establecimiento superen los 750 euros es de 0.1587, una probabilidad baja.

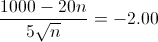




4 comentarios:
EN LA RESPUESTA DE LA PROPOSICIÓN A) DICE CUMPLE PARA n>=54 sin embargo si reemplazo 54 en la desigualdad sale asi: -2 < -2.177 el cual es absurdo...porfavor quisiera aclare mis dudas
Buenas:
Es cierto, ha sido un fallo al poner la expresión, realmente no es una desigualdad, sino que es una igualdad, ya que estamos trabajando con el valor de Φ(z) y el valor obtenido de la probabilidad, es decir:
· Φ(z) = 0.0228 - 0.5 = -0.4772
Donde:
· z = (1000 - 20n)/(5√n)
Sustituimos:
· [Ec1] (1000 - 20n)/(5√n) = - 0.4772
Eso es una igualdad.
Tendremos dos soluciones (ya que es una expresión cuadrática), y la correcta es la que cumpla la condición puesta en: [Ec1].
Ahora bien, al representar n el número de personas, éstas deben ser un número entero, ¿cómo redondeamos?, pues bueno, sabemos que el número de personas, en este caso, debe ser mayor de 53, por lo tanto, el número de personas dadas las condiciones expuestas por el enunciado del problema que mejor se adaptan, es de 54.
Un saludo y gracias por la aclaración.
gracias a ti q me es de bastante utilidad tu blog....ahora si no es mucha molestia como puedo resolver este enunciado: la duración del ciclo de camiones mezcladores y transportadores de concreto que van a la construcción de una carretera se distribuye uniformemente en el intervalo de 50-70 min.calcular cuantos camiones mezcladores se puede programar para esta tarea para q se pueda descargar en el sitio una carga de concreto cada 15 min. ...anticipadamente gracias.
Buenas:
El problema que comentas, por lo menos su enunciado, no es del todo claro, te comento el porqué:
· La variable aleatoria sería la siguiente:
· X ≡ 'Duración del ciclo de camiones mezcladores y transportadores de concreto que van a la construcción de una carretera'
Y ésta sigue una Distribución Uniforme: X ~ U(50, 70) min.
Con esos datos, podemos calcular la media y la varianza:
· μ = (a + b)/2 = (50 + 70)/2 = 60
· σ² = (b - a)²/12 = (70 - 50)²/12 = 100/3
Con esto, podemos decir que, la media de cumplirse un ciclo es de 60 min.
Ahora, me preguntas cuántos camiones mezcladores se pueden programar para tal tarea, cada 15 min.
Vamos a ver, la variable aleatoria que hemos definido así cómo los datos del enunciado, son para dos tipos de procesos:
· Camiones mezcladores y Camiones transportadores.
¿Son los mismos? En caso de que así sea ¿cuántos camiones componen un ciclo?
Supongo que el enunciado del problema lo que realmente quiere pedir, es cuántos camiones (de estos dos tipos) son necesarios para reducir la esperanza de cumplir un ciclo a 15 min.
Recordemos que la esperanza es de 60 min (ya la hemos calculado anteriormente).
En caso de ser así, pues:
· 60 = 15·n
Despejamos:
· n = 60/15 = 4
Hacen falta 4 camiones para reducir la esperanza de la duración del ciclo.
Un saludo.
Publicar un comentario