Problema31: VAC

Ej31. El tiempo (horas) de respuesta de un pedido a cierto proveedor es una variable aleatoria que presenta la siguiente función de densidad:

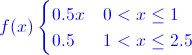
Hallar:

a) Obtener la función de distribución.

b) ¿Qué tiempo es superado por el 50% de los pedidos?.

c) ¿Cuál es el tiempo esperado de un pedido? ¿Cuál es la probabilidad del tiempo esperado?.

d) Un pedido se considera fallido si el tiempo de respuesta es superior a 2.42 horas. Dada una pedido exitoso, ¿cuál es la probabilidad de que su tiempo de respuesta sea superior a 1 hora?.


Apartado a)

Empleamos la expresión de función de distribución acumulada:

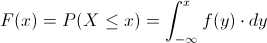
En nuestro caso, debemos realizar el estudio en dos intervalos.

· Primer intervalo: 0 < .x ≤ 1:

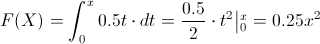
· Segundo intervalo: 1 < .x ≤ 2.5:

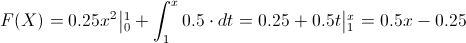
Ya que si x < .0, la función de distribución es 0, y si x > 2.5, la función de distribución es 1, por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:

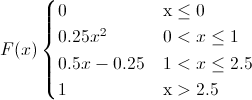
Apartado b)

Suponemos que el 50% de los pedidos está en el intervalo: 1 < .x ≤ 2.5, para ello, empleamos la función de distribución acumulada:

F(X) = 0.5x - 0.25 = 0.5

Despejamos x para obtener el tiempo requerido:

x = 1.5.

Por lo tanto, el tiempo superado por el 50% de los pedidos es 1.5 horas, el cual, podemos comprobar, que la suposición realizada es correcta ya que el resultado está dentro de dicho intervalo.


Apartado c)

En este apartado, debemos calcular la esperanza de la variable aleatoria continua, X.

Para el cálculo de la esperanza, empleamos la siguiente expresión:

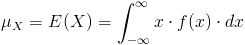
Por lo tanto, la esperanza de X, será:

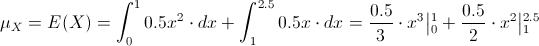
Operamos:

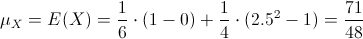
El tiempo esperado de un pedido es, aproximadamente, 1.479167 horas.

Y para calcular la probabilidad de dicho tiempo, empleamos la función de distribución acumulada en el intervalo correcto:

F(71/48) = 0.5·(71/48) - 0.25 = 47/96 ≈ 0.489583.

Apartado d)

Este apartado es de probabilidad condicionada, que para resolverlo, emplearemos la función de distribución acumulada.

Tenemos que tener en cuenta que un pedido se considera fallido si se supera las 2.42 horas.

Lo que debemos obtener es la siguiente probabilidad:

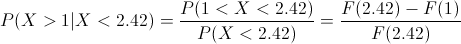
Empleamos la función de distribución acumulada en los intervalos correspondientes:

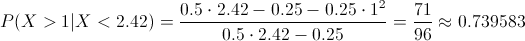
Por lo tanto, la probabilidad de el tiempo de respuesta sea superior a 1 hora dado que sea un pedido exitoso es de, aproximadamente, 0.739583, una probabilidad alta.