Problema76: Estimación y Pruebas de Hipótesis

Ej76. Sea A la duración de un filamento de wolframio en espiral simple, y B la duración usando espiral doble. Se toma una muestra de tamaño 200 de ambos tipos de filamentos teniéndose unas duraciones medias de 1100 horas para A y 1108 horas para B.

Las varianzas de las duraciones de cada tipo de filamento son 20² para A y 23² para B.

Determinar:

a) Construir un intervalo de confianza del 95% para la diferencia de duraciones medias.

b) ¿Hay diferencias significativas entre ambos tipos de filamentos?.


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· A ≡ 'Duración de un filamento de wolframio en espiral simple'. Sigue una distribución Normal: X_A ~ N(1100, 20), n_A = 200.
· B ≡ 'Duración de un filamento de wolframio en espiral doble'. Sigue una distribución Normal: X_B ~ N(1108, 23), n_B = 200.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

Nos piden realizar un intervalo de confianza para la diferencia de medias con varianzas conocidas:

Para un 95%, obtenemos α:

100(1 - α) = 95

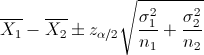
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es 1.96.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la diferencia de medias con un 95%, simplemente, sustituimos valores:

Por lo tanto, el intervalo de confianza requerido por el enunciado del problema es, aproximadamente:

[-12.224243, -3.775757]

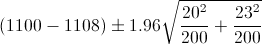
Apartado b)

Simplemente analizando el dato obtenido en el apartado anterior, podemos dar una conclusión sobre ambos tipos de filamentos.

El intervalo de confianza obtenido no contiene el cero, por lo que podemos determinar que existen evidencias significativas para ambos filamentos, en este caso, la duración media de los filamentos en espiral doble serán mayores que los del tipo simple.