Problema54: Estimación y Pruebas de Hipótesis

Ej54. Hasta muy recientemente, p, la tasa de mortalidad causada por una infección vírica del cerebro altamente mortal, la encefalitis producida por el virus del herpes simple, ha sido del 70%.

Se realiza un estudio para probar un nuevo fármaco, la vidarabina, para utilizarlo en el tratamiento de la enfermedad.

Sabiendo que de 50 sujetos en los que se probó la vidarabina, 14 murieron, ¿qué puede decirse sobre la eficacia de este fármaco?.

NOTA: Emplear un nivel de significación del 0.05.


Realizamos una recopilación de datos del problema:

· Tamaño de la muestra: n = 50.
· Individuos que probaron la vidarabina: 14.
· Proporción de de individuos que probaron la vidarabina: ṗ = 14/50 = 0.28.
· Nivel de significación: α = 0.05.
· A ≡ 'Tasa de mortalidad por una infección vírica del cerebro'.
· p(A) = p_o = 0.7.

Nos pide realizar una prueba de hipótesis de proporción, debemos verificar las siguientes condiciones:

· n = 50 ≥ 30 OK.
· n·p_o = 50·0.7 = 35 ≥ 5 OK.
· n·q_o = 50·(1-0.7) = 15 ≥ 5 OK.

La prueba de hipótesis que plantea el enunciado del problema es:

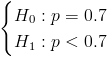
Es un contraste sobre la proporción, el estadístico es:

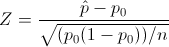
Obtenemos el valor del estadístico:

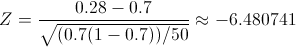
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ -Z_α

Para un nivel de significación de: α = 0.05, tenemos, en la tabla Normal:

· Z_α = Z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:

..1.64.............Z..........1.65
0.4495........0.45.....0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45

Calculamos:

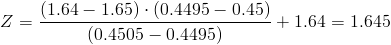
Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, -6.480741 es menor que -1.645 por lo tanto, rechazamos la hipótesis nula.y aceptamos la hipótesis alternativa.

Por lo tanto, esto quiere decir que existen evidencias significativas de que la tasa de mortalidad por una infección vírica del cerebro altamente mortal producida por el herpes simple, es menor del 70% al emplearse el fármaco vidarabina, en otras palabras, podemos concluir que el suministro de dicho fármaco es eficaz ante dicha enfermedad.

Ahora, obtendremos el p-valor, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existe una región crítica, por lo tanto, tenemos una cola de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = P(Z > |z|) = P(Z > 6.480741) ≈ 1 - P(Z ≤ 6.48) = 0.5 - Φ(6.48)

Buscamos en las tablas de la Normal, el valor para 6.48, es: z = 0.5.

Sustituimos y obtenemos el p-valor:

p-valor = 0.5 - Φ(6.48) = 0.5 - 0.5 = 0

Como el p-valor es menor que el nivel de significación, rechazamos la hipótesis nula, y por ende, se acepta la hipótesis alternativa.

Un dato curioso para este estudio es que ante cualquier nivel de significación, siempre se rechazará la hipótesis nula y se aceptará la alternativa, esto es interesante ya que se puede concluir que el uso de dicho fármaco, ayuda y es eficaz ante la enfermedad en cualquier caso.