Problema62: VAD

Ej62. Una caja contiene 30 baterías para radio, de las cuales, 5 son defectuosas. De la caja se escogen al azar 6 baterías, halle la probabilidad de que:

a) 2 sean defectuosas.

b) Ninguna sea defectuosa.

c) Menos de 3 sean defectuosas.

Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº baterías de radio defectuosas'.
· La variable aleatoria X sigue una distribución Hipergeométrica: X ~ HG de parámetros:
· Número total de unidades: N = 30.
· Tamaño de la muestra: n = 5. (Número total de baterías con defectos)
· Número total de unidades seleccionadas aleatoriamente: r = 6.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.

Apartado a)

Debemos hallar la siguiente probabilidad:

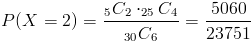
Por lo tanto, la probabilidad de que dos baterías sean defectuosas es de, aproximadamente, 0.213044.

Apartado b)

Debemos hallar la siguiente probabilidad:

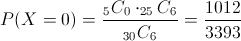
Por lo tanto, la probabilidad de que ninguna de las baterías sean defectuosas es de, aproximadamente, 0.298261.

Apartado c)

Debemos hallar la siguiente probabilidad:

P(X < .3) = P(X = 0) + P(X = 1) + P(X = 2)

Para tal fin, emplearemos el software R:

> sum(dhyper(c(0, 1, 2), 5, 30-5, 6))
[1] 0.9586965

Por lo tanto, la probabilidad de que menos de tres baterías sean defectuosas es de, aproximadamente, 0.958697.